Théorie des langages/Lemme de l'étoile
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 19 Aoû 2008, 16:26
par Anonyme » 19 Aoû 2008, 16:26
Bonjour,
J'aimerais démontrer qu'un langage n'est pas rationnel en utilisant le lemme de l'étoile mais je n'arrive pas à trouver une décomposition correct qui pourrait le démontrer.
Soit le langage L5 = {
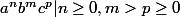
}.
Donc le principe c'est que je suppose que L5 est rationnel, il existe donc un automate déterministe à k états qui le reconnaît.
D'après le lemme de l'étoile
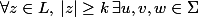
*.
z = uvw tel que |uv|

k, |v| > 0 et
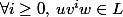
Voilà après je dois trouver un mot que je décompose en uvw avec les contraites énoncées mais je n'arrive pas a trouver.
Est ce que quelqu'un pourrait me dire comment faire et m'expliquer (même me corriger si j'ai fait des erreurs dans ce que j'ai écris) sur cette exemple. Après si j'ai compris je le ferais sur un autre exemple que je pourrais poster une fois réussi.
Merci d'avance.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 19 Aoû 2008, 22:54
par abcd22 » 19 Aoû 2008, 22:54
Bonjour,
L'idée serait d'avoir v constitué de c et prendre i assez grand pour que le nombre de c soit supérieur au nombre de b (donc uv^iw pas dans L). Le problème c'est que les mots sont dans le mauvais sens : avec
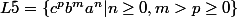
on pourrait appliquer le théorème de Kleene. L'article wikipedia en sur les langages rationnels dit que si L est rationnel « the reverse of L » est aussi rationnel, mais je ne sais pas si « the reverse of L » est le langage constitué des mots de L lus à l'envers ou autre chose.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Aoû 2008, 11:20
par Doraki » 20 Aoû 2008, 11:20
considère le mot m = b^k.c^(k-1).
d'après le lemme de l'étoile, tu as donc m = u.v.w, avec u.v^i.w reconnu par l'automate pour tout i, en particulier pour i = 0
|u.v| <= k donc u.v est composé entièrement de b.
|v| > 0 donc v contient au moins un b.
Donc le mot u.w, qui devrait etre reconnu par l'automate, est de la forme b^k'.c^k-1 avec
k' < k.
Or ces mots ne sont pas dans le langage, et voilà.
-
Anonyme
 par Anonyme » 20 Aoû 2008, 17:20
par Anonyme » 20 Aoû 2008, 17:20
Merci pour ta réponse mais je ne comprends pas du tout, voir même j'ai l'impression que cela n'est pas juste (enfin c'est une impression).
Tu prends le mot
)
, sachant que l'on a la décomposition du mot comme ceci : uvw avec |uv|

k et |v| > 0 donc tu en déduis que uv ne contient que des b. Sachant que l'on "pompe" sur v et qu'il ne possède que des b je ne vois comment on prouve qu'il y a moins de c que de b.
Car l'énoncé dit qu'on a autant de b et c que l'on veut mais avec la contrainte d'avoir moins de c que de b (m > p

0).
Au départ je suis d'accord pour le choix du mot
)
mais c'est après que je ne saisis pas du tout ton raisonnement.
Si tu pouvais être plus précis peut être que je pourrais saisir ton raisonnement.
Merci d'avance.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Aoû 2008, 18:12
par Doraki » 20 Aoû 2008, 18:12
Le but de la manipulation est de donner un mot de ton langage tel que quelle que soit sa décomposition en u.v.w comme décrite dans le lemme, le mot u.w ne soit pas dans le langage et en conclure que L5 n'est pas rationnel.
On part du mot b^k.c^(k-1) (avec le k du lemme)
Combien y a-t-il de b et de c dans v ?
Combien y a-t-il de b et de c dans u.v.w ?
Combien y a-t-il de b et de c dans u.w ?
-
Anonyme
 par Anonyme » 22 Aoû 2008, 15:09
par Anonyme » 22 Aoû 2008, 15:09
Merci maintenant je crois que j'ai compris.
Je l'ai fait aussi avec b^(k+1) c^k => ce qui revient au même.
Logiquement ca devrait aller, merci pour ton aide ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
