Bonsoir tout le monde !
J'étudie actuellement la théorie des graphes et j'aimerais m'avancer dans mon travail estudiantin :) Je fais donc appel à vous pour m'expliquer plusieurs démonstrations que je n'ai pas encore eu le temps de faire, bien entendu.
Voici donc lesdites démonstrations.
1. Montrez qu'un graphe simple a un nombre pair de sommets de degré impair. J'ai ma petite idée : je pense utiliser la formule "la somme des degrés d'un graphe = 2*card(ensemble des arêtes)" en séparant la somme des degrés de sommets à degrés impairs de la somme des degrés de sommets à degrés pairs
mais je ne vois pas trop comment.
2. Démontrez le Lemme de Koenig. Pour rappel, il dit qu'il existe nécessairement une chaîne élémentaire entre deux sommets s1 et s2 reliés par une chaîne quelconque. C'est tellement intuitif que c'en devient impossible à démontrer
3. Démontrez que G connexe comporte au moins card(ensemble des sommets) - 1 arêtes.
4. Démontrez qu'il n'existe pas de graphe non-orienté ayant au moins deux sommets et tel que tous les sommets aient des degrés distincts.
Voilà. J'ai énormément de mal à savoir par où commencer les deux dernières démonstrations
Merci d'avance et bonne continuation.
Théorie des graphes : 4 démonstrations ?
10 messages
- Page 1 sur 1
Je t'aide pour la 1ère question pour l'instant.
Soit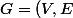) un graphe quelconque avec
un graphe quelconque avec  l'ensemble des sommets et
l'ensemble des sommets et  l'ensemble des arêtes. On note alors :
l'ensemble des arêtes. On note alors :  et
et  .
.
1. On a la formule : = 2m)
2. Soit l'ensemble des sommets de degrés pairs et soit
l'ensemble des sommets de degrés pairs et soit  l'ensemble des sommets de degrés impairs :
l'ensemble des sommets de degrés impairs :  .
.
On a alors :
[CENTER]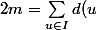 + \underbrace{ \sum \limits_{u \in P} d(u)}_{\text{pair car somme \\ d'entier pair}} \Rightarrow \underbrace{\sum \limits_{u \in I} d(u)}_{\text{pair}} = \underbrace{2m - \sum \limits_{u \in P} d(u)}_{\text{pair}}) [/CENTER]
[/CENTER]
Or ,
, ) est impair. Une somme d'entiers impairs et pair s'il y a un nombre pair (ou nul) d'entiers.
est impair. Une somme d'entiers impairs et pair s'il y a un nombre pair (ou nul) d'entiers.
Conclusion : Le nombre de sommets de degrés impair est pair.
Soit
1. On a la formule :
2. Soit
On a alors :
[CENTER]
Or
Conclusion : Le nombre de sommets de degrés impair est pair.
Merci beaucoup l'ami !
J'ai juste une petite question sur la conclusion.
Or \forall u \in I, d(u) est impair. Une somme d'entiers impairs eS(?)t pair s'il y a un nombre pair (ou nul) d'entiers.
Conclusion : Le nombre de sommets de degrés impair est pair.
===> c'est bien parce que la somme d'entiers impairs qu'on utilise est, d'après ce qu'on a trouvé, TOUJOURS paire ? Alors qu'elle n'est paire que s'il y a un nombre pair ou nul d'entiers ?
C'est ça ? ^^
J'ai juste une petite question sur la conclusion.
Or \forall u \in I, d(u) est impair. Une somme d'entiers impairs eS(?)t pair s'il y a un nombre pair (ou nul) d'entiers.
Conclusion : Le nombre de sommets de degrés impair est pair.
===> c'est bien parce que la somme d'entiers impairs qu'on utilise est, d'après ce qu'on a trouvé, TOUJOURS paire ? Alors qu'elle n'est paire que s'il y a un nombre pair ou nul d'entiers ?
C'est ça ? ^^
oui c'est un "est" et non pas "et"
On sait que la somme des degrés des sommets impairs est pair.
Or, pour avoir une somme pair avec des entiers impairs il te faut un nombre pairs d'entiers.
edit : tes sérieux la ? :ptdr: :ptdr: lien
On sait que la somme des degrés des sommets impairs est pair.
Or, pour avoir une somme pair avec des entiers impairs il te faut un nombre pairs d'entiers.
edit : tes sérieux la ? :ptdr: :ptdr: lien
Pour le lemme de koenig : http://idmme06.inpg.fr/~rapinec/Graphe/Chemin/elementaire.html
(tout en bas)
(tout en bas)
Pour le dernier, on résonne par l'absurde :
Supposons qu'il existe un graphe G qui possède n sommets et dont le degrés de tous les sommets est différents.
Le degré maximal d'un sommet est n - 1 (un sommet est voisin avec tous les autres).
Tous sommets ont donc un degré différent comprit entre 0 et n - 1.
Le premier sommet a 0 voisin
Le deuxième a 1 voisin
...
Le n-ième à n - 1 voisins
Or si le premier sommet à 0 voisin, le n-ième sommet ne peut pas avoir n - 1 voisins. Donc c'est impossible.
Supposons qu'il existe un graphe G qui possède n sommets et dont le degrés de tous les sommets est différents.
Le degré maximal d'un sommet est n - 1 (un sommet est voisin avec tous les autres).
Tous sommets ont donc un degré différent comprit entre 0 et n - 1.
Le premier sommet a 0 voisin
Le deuxième a 1 voisin
...
Le n-ième à n - 1 voisins
Or si le premier sommet à 0 voisin, le n-ième sommet ne peut pas avoir n - 1 voisins. Donc c'est impossible.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
