Théorème du point fixe !

par **barbu23** » 03 Aoû 2007, 23:06

Bonsoir:
Soit:

tel que :

converge.
Soit

un espace metrique complet.
Soit:

:

une application pour laquelle :

:

.
Montrer que

possède un point fixe unique :

.
Merçi d'avance !!!

par **barbu23** » 03 Aoû 2007, 23:14

Si

et

sont deux points fixes de

alors :

et

.

:

.
Merçi d'avance !!

par **Imod** » 03 Aoû 2007, 23:15

Je ne réponds pas aux questions de cours et je fais beaucoup de fautes mais je préfère "merci" sans la cédille :we:

Merci d'avance !!!

Imod

par **barbu23** » 03 Aoû 2007, 23:22

va y, donne des idées... !!

par **barbu23** » 03 Aoû 2007, 23:27

C'est pas une question de cours ça, c'est un exercice !!

par **barbu23** » 04 Aoû 2007, 00:01

:

(absurde).
Donc il existe un seul point fixe de

.

par **legeniedesalpages** » 04 Aoû 2007, 00:03

Peut-être une idée pour l'unicité du point fixe:

En admettant que f possède un point fixe x, montrer que toute suite définie de la façon suivante a pour limite x:

un point de x,

quelque soit l'entier n.

Si il y aurait deux points fixes distincts x et y, ces suites convergeraient alors vers deux valeurs distinctes ce qui est absurde vu que X est séparé (un espace métrique est automatiquement séparé).

Pour montrer l'existence de ce point fixe, il me semble qu'il faut utiliser le fait que X est complet et les propriétés liées à la distance.

par **legeniedesalpages** » 04 Aoû 2007, 00:07

Barbu23, ta démo me semble correcte, mais tu devrais pas utiliser à tout va les symboles

, tu diminues la clarté de rédaction et ça peut amener à des confusions.

Sinon tu as montrer que si il existe un point fixe de f, il n'en existe pas d'autres (unicité).
Mais tu n as pas montré qu'il en existe au moins un (existence).

par **barbu23** » 04 Aoû 2007, 00:10

Ben moi j'ai utilisé la même methode du cours : arriver à une contradiction de type : supposons , par absurde, que

et

sont deux points fixes de

( contradiction ).

par **barbu23** » 04 Aoû 2007, 00:11

Mais c'est pas demandé dans l'exercice "legeniedesalpages" !!

par **barbu23** » 04 Aoû 2007, 00:16

Ah oui tu as raison "legeniedesalpages", comme dans la demonstration du cours !!

par **legeniedesalpages** » 04 Aoû 2007, 00:19

barbu23 a écrit:Montrer que possède un point fixe unique : .

par "possède", je pense qu'on te demande de montrer qu'il en a au moins un, et par "unique", qu'il en possède pas plus d'un.

Donc tu as deux choses à démontrer.

par **Edrukel** » 04 Aoû 2007, 09:50

l'idée est de supposer qu'il yen a deux l et l' et en utilisant la notion de la distance avec les résultats précédents de montrer que l=l'

par **kazeriahm** » 04 Aoû 2007, 10:55

pour montrer l'existence d'un point fixe, définit une suite récurrente

x_0 dans X et x_n+1=f(x_n)

essayer de montrer que (x_n) est de Cauchy dans X complet donc convergente (ceci grace à l'inégalité donnée)

(x_n) converge, vers un point fixe de f...

par **kazeriahm** » 04 Aoû 2007, 11:05

je détaille

on a

on veut montrer que

est de Cauchy

La suite

étant à terme positifs, on a

[TEX]d(x_p,x_{p+k}) \leq d(x_1,x_0) \displaystyle{\sum_{i=p}^{\infty} a_i}[\TEX]

et la somme est le reste d'une série convergente, qui tend donc vers 0 quand p tend vers l'infini

donc la suite (x_n) est de Cauchy

par **kazeriahm** » 04 Aoû 2007, 11:09

je détaille

on a

on veut montrer que

est de Cauchy

La suite

étant à terme positifs, on a

et la somme est le reste d'une série convergente, qui tend donc vers 0 quand p tend vers l'infini

donc la suite (x_n) est de Cauchy

EDIT : bon le TEX passe pas au milieu je comprends pas... si un admin passe par ici, s'il peut regarder...

EDIT2: merci geniedesalpages :marteau:

par **legeniedesalpages** » 04 Aoû 2007, 11:21

il faut fermer par cette balise : [/TEX], et non par celle là: [\TEX] :ptdr:

par **barbu23** » 04 Aoû 2007, 21:43

Merçi à vous tous pour les reponses que vous m'avez donnés ...!
J'ai deux autres questions à vous poser concernant le même sujet ... !
Ma première question est:
Est ce que si on prend deux points distincts

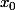
et

, alors on aura deux points fixes distincts

et

de

avec :

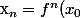et

.
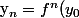Ma seconde question est:
Quant on essaye de démontrer "l'existence" d'un point fixe de

, on considère un point quelconque :

de :

, et la suite réccurente définie par :

...On montre que :

est de Cauchy donc convergente puisque

est complet, et converge vers un élément

qui est obtenu en iterant à l'infini l'image de

par

,et qui est un point fixe de

biensûr.
Si on fait la même chose avec un autre point

, on obtient un autre point fixe

...et ainsi de suite avec tous les éléments de

...Est ce que celà veut dire que pour tous point de

, il existe un point fixe qui lui correspond par

.Est ce que celà est vrai ?!
Merçi d'avance !!!

par **yos** » 04 Aoû 2007, 22:00

Bonsoir.
On a prouvé qu'il y a un seul point fixe p. Donc pour tout x,

.
Pour ta deuxième question, n'extrapole pas trop : il faut des hypothèses sur f.

par **barbu23** » 04 Aoû 2007, 23:14

D'accord, merçi Yos..!
C'est joli ça:

:

...
Maintenant, je comprends bien le sens de l'unicité du point fixe de

.

Théorème du point fixe !

Théorème du point fixe !

Qui est en ligne