Taux d'accroissement avec Ln

[Oplya]

Bonsoir,

Je dois montrer qu'une fonction est dérivable en 0, donc j'ai fait le taux d'accroissement quand x tend vers 0.

Cette fonction c'est Ln (exp(x) - 1 / x). Cette fonction est définie sur R +,*. Dans les questions précédentes je devais faire la continuité en 0. Alors j'ai dérivé celle-ci en 0, puis j'ai prolongé avec une nouvelle fonction qui inclue f(0) = 0.
Pour revenir à mon énoncé, j'ai fait le taux d'accroissement en 0. Je tombe sur Ln (exp(x) - 1 / x) / x. Ma première solution c'était de dire que Ln (exp(x) - 1 / x) était négligeable devant x lors que x tend vers 0. Par conséquent la limite serait 0. C'est une limite finie mais cela voudrait dire que la tangente serait horizontale, je doute un peu :hein:.
Ensuite j'ai mis toute la fonction c'est-à-dire Ln (exp(x) - 1 / x) / x en puissance de l'exponentielle. Ce qui donne : Exp (Ln (exp(x) - 1 / x) / x) puis Exp ( Ln (exp(x) - 1 / x)) - Exp(x) = (Exp(x) - 1 / x) - Exp (x). Là je trouve une limite qui est de 1. Là je suis encore plus perdu !

Merci pour toutes aides !

[BiancoAngelo]

Bonsoir,

Je dois montrer qu'une fonction est dérivable en 0, donc j'ai fait le taux d'accroissement quand x tend vers 0.

Cette fonction c'est Ln (exp(x) - 1 / x). Cette fonction est définie sur R +,*. Dans les questions précédentes je devais faire la continuité en 0. Alors j'ai dérivé celle-ci en 0, puis j'ai prolongé avec une nouvelle fonction qui inclue f(0) = 0.
Pour revenir à mon énoncé, j'ai fait le taux d'accroissement en 0. Je tombe sur Ln (exp(x) - 1 / x) / x. Ma première solution c'était de dire que Ln (exp(x) - 1 / x) était négligeable devant x lors que x tend vers 0. Par conséquent la limite serait 0. C'est une limite finie mais cela voudrait dire que la tangente serait horizontale, je doute un peu :hein:.
Ensuite j'ai mis toute la fonction c'est-à-dire Ln (exp(x) - 1 / x) / x en puissance de l'exponentielle. Ce qui donne : Exp (Ln (exp(x) - 1 / x) / x) puis Exp ( Ln (exp(x) - 1 / x)) - Exp(x) = (Exp(x) - 1 / x) - Exp (x). Là je trouve une limite qui est de 1. Là je suis encore plus perdu !

Merci pour toutes aides !

Tu es sûr de ta fonction ? Elle n'est pas définie sur R+*, ça se voit d'entrée, car la limite de -1/x en 0 est -infini...

En effet, il faut que exp(x) - 1/x > 0...
Donc forcément que ça fait n'importe quoi si ce n'est pas défini

[BiancoAngelo]

Mince je viens de comprendre que c'est ln ( (exp(x) - 1) /x) :marteau:

[zygomatique]

salut

[Oplya]

salut

Bonsoir, je ne comprend pas cette écriture, je ne l'ai jamais étudié auparavant.

[capitaine nuggets]

Bonsoir,

Je dois montrer qu'une fonction est dérivable en 0, donc j'ai fait le taux d'accroissement quand x tend vers 0.

Cette fonction c'est Ln (exp(x) - 1 / x). Cette fonction est définie sur R +,*. Dans les questions précédentes je devais faire la continuité en 0. Alors j'ai dérivé celle-ci en 0, puis j'ai prolongé avec une nouvelle fonction qui inclue f(0) = 0.
Pour revenir à mon énoncé, j'ai fait le taux d'accroissement en 0. Je tombe sur Ln (exp(x) - 1 / x) / x. Ma première solution c'était de dire que Ln (exp(x) - 1 / x) était négligeable devant x lors que x tend vers 0. Par conséquent la limite serait 0. C'est une limite finie mais cela voudrait dire que la tangente serait horizontale, je doute un peu :hein:.
Ensuite j'ai mis toute la fonction c'est-à-dire Ln (exp(x) - 1 / x) / x en puissance de l'exponentielle. Ce qui donne : Exp (Ln (exp(x) - 1 / x) / x) puis Exp ( Ln (exp(x) - 1 / x)) - Exp(x) = (Exp(x) - 1 / x) - Exp (x). Là je trouve une limite qui est de 1. Là je suis encore plus perdu !

Merci pour toutes aides !

Ton premier raisonnement m'a l'air bon.
Le deuxième, si tu composes avec exp au début, tu dois recomposer avec ln a la fin :+++:

[BiancoAngelo]

Bonsoir,

Ensuite j'ai mis toute la fonction c'est-à-dire Ln (exp(x) - 1 / x) / x en puissance de l'exponentielle. Ce qui donne : Exp (Ln (exp(x) - 1 / x) / x) puis Exp ( Ln (exp(x) - 1 / x)) - Exp(x) = (Exp(x) - 1 / x) - Exp (x).

Ici, ça ne va pas, n'est pas

[BiancoAngelo]

Je pense plutôt que comme on a et que l'intérieur tend vers 1, il faut plutôt poser :



Vérifier que g est dérivable en 0, et comme X -> ln(X) n'a pas de problème de dérivabilité en X = 1, ce serait réglé.

[BiancoAngelo]

C'est vrai que cette histoire est compliquée sans les DL.

Je ne sais pas trop si on peut dire que :

Soit .

Son taux d'accroissement en 0 est défini par

et on sait que la limite en 0 existe (cf. exp est dévirable).

Maintenant, je me demande si de la même façon, on peut prendre le taux d'accroissement en 0 du taux d'accroissement en 0... et écrire que c'est :

et dont la limite existe (cf. exp deux fois dérivable).

Donc g(x) bien dérivable en 0...

Or, on a posé g(0) = 1 et comme ln n'a pas de problème de dérivabilité en 1, ça donne bien ce qu'on cherche...


Bon, arrêtez moi si je dis des bêtises :ptdr: :mur:

[Ben314]

Perso, ce que je comprend pas (ormis bien entendu le fait qu'en post bac on puisse encore ne pas savoir que la division est prioritaire sur l'addition... ), c'est pourquoi "l'ensemble de définition de f est ".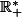
n'est pas positif pour tout x ?

[BiancoAngelo]

Perso, ce que je comprend pas (hormis bien entendu le fait qu'en post bac on puisse encore ne pas savoir que la division est prioritaire sur l'addition... ), c'est pourquoi "l'ensemble de définition de f est ".
n'est pas positif pour tout x ?

C'est p'tet la restriction que choisit l'exercice. :doh:

Et pourquoi tu parles de priorité de la division ?

[Ben314]

C'est p'tet la restriction que choisit l'exercice. :doh:

p'tet...
ou alors il s'est gouré dans l'ensemble de définition...
Comme il vaut mieux être prudent... :marteau:

[BiancoAngelo]

p'tet...
ou alors il s'est gouré dans l'ensemble de définition...
Comme il vaut mieux être prudent... :marteau:

Et ce que j'ai raconté avec le taux du taux... Ca tient la route ?

[chombier]

Et ce que j'ai raconté avec le taux du taux... Ca tient la route ?

Le "taux du taux" est bien une fonction, donc étudiable, mais je ne pense pas qu'elle soit très exploitable

[Ben314]

et dont la limite existe (cf. exp deux fois dérivable).

Donc g(x) bien dérivable en 0...

ça, au fond, c'est correct, mais pour le justifier sans les D.L., je pense que c'est un peu chiant vu qu'en fait, ton , c'est .

[Oplya]

Perso, ce que je comprend pas (ormis bien entendu le fait qu'en post bac on puisse encore ne pas savoir que la division est prioritaire sur l'addition... ), c'est pourquoi "l'ensemble de définition de f est ".
n'est pas positif pour tout x ?

C'est la restriction de l'exercice.

[BiancoAngelo]

ça, au fond, c'est correct, mais pour le justifier sans les D.L., je pense que c'est un peu chiant vu qu'en fait, ton , c'est .

Et cette fraction justement, elle n'est pas sensée avoir une limite si justement la fonction de base est dérivable deux fois ? Et même tendre vers f''(0) ?

Je n'avais jamais fait le taux du taux comme ça, c'est vrai qu'on se balade toujours avec les DL...

[chombier]

Et cette fraction justement, elle n'est pas sensée avoir une limite si justement la fonction de base est dérivable deux fois ? Et même tendre vers f''(0) ?

Je n'avais jamais fait le taux du taux comme ça, c'est vrai qu'on se balade toujours avec les DL...

Il y a de l'idée, mais ce n'est pas exactement ça, et je ne suis pas hyper sur de moi. J'explique :

Attention : Dans ce post, représente une fonction qui tend vers 0 quand x tend vers 0, mais ce n'est pas toujours la même fonction (je me donne le droit d'écrire )

On suppose donc la fonction f dérivable deux fois en 0.

[BiancoAngelo]

Il y a de l'idée, mais ce n'est pas exactement ça, et je ne suis pas hyper sur de moi. J'explique :

Attention : Dans ce post, représente une fonction qui tend vers 0 quand x tend vers 0, mais ce n'est pas toujours la même fonction (je me donne le droit d'écrire )

On suppose donc la fonction f dérivable deux fois en 0.

Effectivement, à cause du 2!, ça donne bien ça.
Étrange vu que c'est le taux d'un taux...

[chombier]

Effectivement, à cause du 2!, ça donne bien ça.
Étrange vu que c'est le taux d'un taux...

Faux arrêter avec cette histoire de "taux d'un taux", ou alors il faut formaliser ça correctement !