Tangente en l'infini

[Lucas1995]

Bonsoir à tous,
Je viens d'entrer en MPSI et 1er DM que j'ai du mal à rédiger rigoureusement, voici mon soucis en simplifié :
peut-on considérer qu'il existe une tangente à la fonction carré perpendiculaire à D:y=0 ?
En fait, je me demande si on peut considérer qu'il existe un point M de Cf de coordonnées (x;x²) pour lesquelles on fait tendre x vers l'infini.
Mais ça manque peut-être de rigueur ...
Merci d'avance !

[Luc]

Salut,
la fonction x-> x^2 a une propriété remarquable : elle est convexe, c'est-à-dire qu'elle reste toujours au-dessus de ses tangentes. Si tu supposes qu'il existe une tangente perpendiculaire à l'axe y=0, une telle tangente est verticale, donc d'équation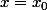 . Cette droite traverse la courbe, c'est impossible par convexité.
Autre méthode : Soit T la tangente à la courbe en . Son coefficient directeur est . Donc son équation ne peut pas être de la forme x=constante.

En fait, intuitivement, si tu fais "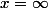", tu obtiens effectivement une tangente verticale à la courbe. Mais un tel point n'est pas dans le plan euclidien.
Par contre en géométrie projective c'est autre chose... (on rajoute un point à l'infini).

[Lucas1995]

Merci bien c'est exactement la réponse que j'espérais :)
Bonne soirée !