Tan(x)=x, somme d'une série.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 23 Aoû 2009, 14:42
par skilveg » 23 Aoû 2009, 14:42
Peut-être mais je n'y crois pas trop, je n'ai pas vu apparaître le sacro-saint 691 :langue2: Si c'était le cas cela indiquerait un lien probable avec la fonction
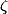
, mais encore faudrait-il le trouver.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 24 Aoû 2009, 16:53
par Pythales » 24 Aoû 2009, 16:53
Pour répondre à la question 17 de Skilveg, j'ai démontré que les équations
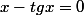
(1)
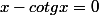
(2)
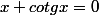
(3)
ont toutes leurs racines

réelles.
On trouve
Pour (1)

Pour (2)

Pour (3)

(par Excel)
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 24 Aoû 2009, 17:52
par skilveg » 24 Aoû 2009, 17:52
Du coup, ton problème reste entier: pourquoi trouve-t-on
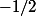
? Les racines réelles font converger la série, ce n'est donc a priori pas un problème de divergence.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 26 Aoû 2009, 12:31
par Pythales » 26 Aoû 2009, 12:31
Si l'on en croit Yos (réponse #7), ce serait Hadamard qui aurait travaillé là-dessus.
Avez-vous d'autres informations à ce sujet ?
Merci d'avance.
-
mathelot
 par mathelot » 11 Oct 2009, 14:12
par mathelot » 11 Oct 2009, 14:12
-
Borriello
- Messages: 8
- Enregistré le: 07 Oct 2009, 15:30
-
 par Borriello » 11 Oct 2009, 14:32
par Borriello » 11 Oct 2009, 14:32
Doraki a écrit:Hmm on peut dire que
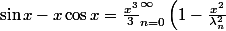)
et calculer la dérivée 5ème de ces choses ?
Mais j'imagine que l'analyse complexe nécessaire pour faire tout ça n'est pas plus élémentaire que la théorie des résidus.
En fait, on n'a que
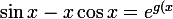}\frac{x^3}{3}\Bigprod_{n=0}^{\infty}\left(1-\frac{x^2}{\lambda_n^2}\right))
où g est une fonction entière sur

Il faut encore démontrer que
)
= constante. C'est pas facile du tout :mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
