DM sur la convergence des suites

[deltab]

Bonsoir.

Étudies sur ]0,1] les deux fonctions et

[Robic]

L'énoncé ne serait pas plutôt : 1+x
Je sais, si on démontre que exp(x) est plus petit que 1+x+x²/2, du coup il sera plus petit que <1+x+x². Mais ça permet surtout de pouvoir étudier la variation de la fonction x-->exp(x)-(1+x+x²/2). En effet, sa dérivée fait intervenir la fonction x-->exp(x)-(1+x) qui a été étudiée juste avant. On voit ainsi que x-->exp(x)-(1+x+x²/2) est croissante et il suffit de la calculer en 0 pour avoir le résultat demande sur ]0,1].

S'il n'y a pas d'erreur d'énoncé, eh bien... démontre d'abord que exp(x)<1+x+x²/2 et déduis-en que exp(x)<1+x+x².

[Robic]

(Oups, j'ai lu trop vite.)

[adrien69]

Comparaison série-intégrale :)

[adrien69]

C'est pas une question de revoir. C'est une question de savoir dessiner, et de savoir intégrer 1/x².
Voilà le genre de dessins qu'il faut faire !

[Robic]

Il y a plus simple (et du coup j'ai effacé trop vite ma réponse précédente) :

- On majore chaque terme par 1/n² (à justifier).
- Du coup... le résultat est immédiat.

[Monsieur23]

Aloha,

[quote="Robic"]L'énoncé ne serait pas plutôt : 1+xexp(x)-(1+x+x²/2). En effet, sa dérivée fait intervenir la fonction x-->exp(x)-(1+x) qui a été étudiée juste avant. On voit ainsi que x-->exp(x)-(1+x+x²/2) est croissante et il suffit de la calculer en 0 pour avoir le résultat demande sur ]0,1].

S'il n'y a pas d'erreur d'énoncé, eh bien... démontre d'abord que exp(x)1+x+x²/2 !

[Robic]

Ah mais oui, tu as raison ! Dommage, on pouvait plus facilement faire les calculs...

Donc pour prouver que e^x-(1+x+x²) est positif, il faut étudier ses variations, et pour ce faire il faut étudier les variations de la dérivée c'est-à-dire les variations de x --> e^x-(1+2x), et pour ce faire il faut étudier, donc dériver, cette dernière fonction. Et cette fois ça marche : la dérivée est croissante de 0 à ln2 et décroissante de ln2 à 1, il y a donc un maximum et celui-ci est négatif, donc la dérivée est toujours négative, ce qui prouve que la fonction de départ est décroissante, donc plus petite que f(0) qui vaut 0, donc négative, ouf !

[adrien69]

Il y a plus simple (et du coup j'ai effacé trop vite ma réponse précédente) :

- On majore chaque terme par 1/n² (à justifier).
- Du coup... le résultat est immédiat.

Auquel cas il vaut mieux utiliser 1/((n+1)n) comme majorant. Sachant que 1/((n-1)n)=1/n-1/(n+1) on a une série téléscopique et on est repus.

[deltab]

Bonjour.

Auquel cas il vaut mieux utiliser 1/((n+1)n) comme majorant. Sachant que 1/((n-1)n)=1/n-1/(n+1) on a une série téléscopique et on est repus.

L'indication "il vaut mieux utiliser 1/((n+1)n) comme majorant" risque de ne pas être bien comprise, il valait préciser la majoration à faire ou plus donner d'indications, et on obtiendra une somme (et non série) télescopique.
La majoration de chaque terme par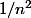 est quand même la méthode la plus simple.