Suite et Série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Tigrana
- Messages: 1
- Enregistré le: 07 Déc 2010, 09:53
-
 par Tigrana » 07 Déc 2010, 10:16
par Tigrana » 07 Déc 2010, 10:16
Bonjour,
J'ai un exercice pour un DM que je n'arrive pas à faire :
Soit
)
et
)
deux suites de nombres réels. On suppose
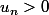
et
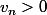
pour tout
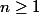
et qu'il existe un entier
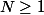
tel que :

pour tout
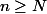
1) Montrer qu'on a :

pour tout
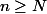
2) En déduire que, si la série

converge, alors la série

converge.
Merci d'avance pour l'aide !!
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Déc 2010, 12:18
par Arnaud-29-31 » 07 Déc 2010, 12:18
Salut,
La question 1) revient à montrer que

,

.
Or tu sais que

,

Donc



...

-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 07 Déc 2010, 13:18
par arnaud32 » 07 Déc 2010, 13:18
1) puisque les suites sont positives l'hyp devient que w(n)=u(n+N)/v(n+N) est decroissante donc tous les termes sont inferieurs au premier
2)
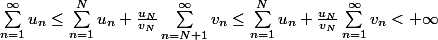
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités