bonjour
je rencontre quelques difficultés à montrer la chose suivante
la suite de fibonacci est définie par f0=0 f1=1 et fn+2=fn+1+fn
j'ai déjà montrer la relation de cassini fn+1fn-1-fn^2=(-1)^n
mais je n'arrive pas à montrer fm+n=fmfn+fm-1fn-1
je pense à une récurrence en fixant m ou n mais je ne m'en sors pas
votre aide est la bien venue
merci
Suite de fibonacci
8 messages
- Page 1 sur 1
Salut.
Je fais une récurrence sur m.
"pour tout entier naturel n" est partout sous-entendu.
a) Pour m=0, c'est la relation connue.
b) On suppose la relation vraie jusqu'à l'entier m.
}=f_{m+n}+f_{m+n-1}\\<br />=(f_mf_n+f_{m-1}f_{n-1})+(f_mf_{n-1}+f_{m-1}f_{n-2})\\<br />=f_mf_n+f_{m-1}(f_{n-1}+f_{n-2})+f_mf_{n-1}\\<br />=f_mf_n+f_{m-1}f_{n}+f_mf_{n-1}\\<br />=f_m(f_{n}+f_{n-1})+f_{m-1}f_{n}\\<br />=f_mf_{n+1}+f_{m-1}f_{[(n+1)-1]})
Ce qui achève la récurrence.
On peut aussi le prouver à partir de la formule explicite de fn :
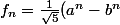) où a et b sont les racines de x²-x-1.
où a et b sont les racines de x²-x-1.
Je fais une récurrence sur m.
"pour tout entier naturel n" est partout sous-entendu.
a) Pour m=0, c'est la relation connue.
b) On suppose la relation vraie jusqu'à l'entier m.
Ce qui achève la récurrence.
On peut aussi le prouver à partir de la formule explicite de fn :
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
