Sous-suites paires et sous-suites impaires !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
forza
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Sep 2006, 18:14
-
 par forza » 28 Déc 2006, 23:43
par forza » 28 Déc 2006, 23:43
Je voyait le bout du DM arrivait mais cette question me bloque ;-)
On a U0=0 et Un+1 = Un²+A
Ici on suppose que A est un reel avec -1
Montrez que la suite ( U2n) est decroissante et que (U2n+1) est croissante
J'ai essayer de calculer U2n+2-U2n mais j'arrive sur des carrés de soous suites impaires pas top je pense
J'ai essayer par recurrence :
Je suppose que U2n+2>U2n
Je montre que U2n+4>U2n+2
Meme probleme enfin selon moi ;-)
Quelqu'un peut t'il m'aider ?
Merci d'avance
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Déc 2006, 00:11
par Nightmare » 29 Déc 2006, 00:11
Bonsoir
Par exemple :
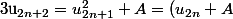^{2}+A=u_{2n}^{2}+2u_{2n}+A^{2}+A)
Ainsi :
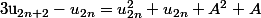
Soit X²+X+A²+A le polynôme d'indeterminée X.
Son discriminant vaut -4A(A+1)
Or lorsque -1<A<0, ce discriminant est négatif et donc le trinôme est positif.
Conclus

-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 29 Déc 2006, 02:33
par BQss » 29 Déc 2006, 02:33
[quote="Nightmare"]Bonsoir
Par exemple :
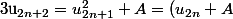^{2}+A=u_{2n}^{2}+2u_{2n}+A^{2}+A)
Ainsi on pose X=u(n)^2 :
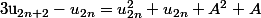
Soit X²+X+A²+A le polynôme d'indeterminée X.
Son discriminant vaut -4A(A+1)
Or lorsque -1 A -1|X+A|0<(X+A)^2<-A donc finalement :
A<(X+A)^2+A<0 soit -1<A<u(2n+2)<0
Ce qui acheve la recurrence. C'est a dire que tout u2n est compris entre A et 0.
Par contre je viens de voir il me semble que meme si u2n est compris entre A et 0 le polynome peut etre positif, donc il faudrait encore resteindre l'intervalle ou alors utiliser une autre methode.
Bon j'me taillos a plus.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 29 Déc 2006, 10:26
par fahr451 » 29 Déc 2006, 10:26
la méthode est générale peu importe l'expression de f ;
f(x) = x^2+ A
u(n+1) = f(u(n)) en prenant I = [-1,0]
I est stable par f ( f(I) inclus ds I) u(0) est dans I ,donc u est à valeurs dans I
f décroit sur I mais g = f0f croit sur I et les sous suites v(n)= u(2n) et
w(n) = u(2n+1) vérifient la relation
v(n+1)= g(v(n)) ; w(n+1) = g(w(n)) ;
I est stable par g ; g croit sur I donc v et w sont monotones (monotonie inverse) .
pour savoir si v croit il suffit de comparer v(1) = u(2) à v(0) = u(0).
-
forza
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Sep 2006, 18:14
-
 par forza » 29 Déc 2006, 11:16
par forza » 29 Déc 2006, 11:16
C dans la question suivante qu'il parle de fof donc je ne pense pas qu'il faille utiliser cette methode !!
Avec le discriminant ou avec la recurrence ! Cela ne fonctionne t'il pas ? car a la fin BQss tu as sous entend que ce que tu avais fait étais pas bon car le polynome pouvait etre positif, j'ai pas compris cela
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 29 Déc 2006, 11:26
par fahr451 » 29 Déc 2006, 11:26
ce que j'ai dit n'est malheureusement pas correct car[-1,0] n'estpas stable par f . donc on ne peut pas utiliser la monotonie de f
en revanche
I =[A,0] est stable par f et on est sauvé.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 29 Déc 2006, 11:39
par fahr451 » 29 Déc 2006, 11:39
->forza bien sûr la récurrence c'est la méthode que je propose (elle est générale)
I= [A,0] est stable par f c 'est le point essentiel
u(0) est dans I on montre par récurrence (immédiate) u(n) dans I
v,w sont dans I (stable par f )et comme g croit on montre qu'elles sont monotones.
par récurrence sur n on montre v(n+1) =on vérifie pour n = 0 et ensuite en le supposant pour n en appliquant g croissante sur I on a le résultat pour n+1.
si tu ne veux pas utiliser g utilise donc f puis encore f ...
Le seul point qui compte c 'est avoir I stable par f sur lequel f est décroissante.
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 29 Déc 2006, 11:43
par BQss » 29 Déc 2006, 11:43
fahr451 a écrit:la méthode est générale peu importe l'expression de f ;
f(x) = x^2+ A
u(n+1) = f(u(n)) en prenant I = [-1,0]
I est stable par f ( f(I) inclus ds I) u(0) est dans I ,donc u est à valeurs dans I
f décroit sur I mais g = f0f croit sur I et les sous suites v(n)= u(2n) et
w(n) = u(2n+1) vérifient la relation
v(n+1)= g(v(n)) ; w(n+1) = g(w(n)) ;
I est stable par g ; g croit sur I donc v et w sont monotones (monotonie inverse) .
pour savoir si v croit il suffit de comparer v(1) = u(2) à v(0) = u(0).
Ca me revient maintenant, on avance par collimasson de part et d'autre du point fixe en s'en rapprochant. On peut meme dire que si la courbe est au dessus de x sur I stable alors la fonction est croissante.
-
forza
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Sep 2006, 18:14
-
 par forza » 29 Déc 2006, 11:45
par forza » 29 Déc 2006, 11:45
j'ai compris ;-) merci bcp a vous 2 !!!!!
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 29 Déc 2006, 11:46
par BQss » 29 Déc 2006, 11:46
Ca me revient ta methode fahr , on avance en collimasson de part et d'autre du point fixe en s'en rapprochant et on a meme quand I stable et f au dessus de y=x --> un croissante..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
