Soucis factorisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Amandinefch
- Messages: 7
- Enregistré le: 25 Oct 2015, 11:14
-
 par Amandinefch » 25 Oct 2015, 11:26
par Amandinefch » 25 Oct 2015, 11:26
Bonjour à tous,
Voilà j'ai un DM à faire pour la rentrée en maths bien sûr, mais je rencontré un petit problème. Je vous explique :
Après avoir résolu les limites de cette équation (exp^(2x) - 2x - 1), je dois maintenant étudier les variations de celle-ci. Cependant il faut pour cela calculer sa dérivée. Et là est mon problème !!! Comment mettre 2x en facteur pour ainsi pouvoir en déduire les variations ?
Merci à ceux et celles qui me répondront, en vous souhaitant une bonne journée et de bonnes vacances pour ceux qui y sont ! ;)
-
mathelot
 par mathelot » 25 Oct 2015, 11:35
par mathelot » 25 Oct 2015, 11:35
une petite astuce
=2e^{2x}-2)
puis calcule f''
Le signe de f'' te permet de remonter aux variations de f.
-
Amandinefch
- Messages: 7
- Enregistré le: 25 Oct 2015, 11:14
-
 par Amandinefch » 25 Oct 2015, 11:40
par Amandinefch » 25 Oct 2015, 11:40
Merci !
C'est ce que j'avais fait pour f'(x), mais je n'ai jamais étudier f'' ! Vous venez de me l'apprendre !
-
mathelot
 par mathelot » 25 Oct 2015, 11:46
par mathelot » 25 Oct 2015, 11:46
Amandinefch a écrit:Merci !
C'est ce que j'avais fait pour f'(x), mais je n'ai jamais étudier f'' ! Vous venez de me l'apprendre !
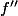
est la dérivée de

.
Ici,
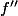
est trivialement strictement positive donc f' est croissante strictement.
Que vaut
)
?
-
Amandinefch
- Messages: 7
- Enregistré le: 25 Oct 2015, 11:14
-
 par Amandinefch » 25 Oct 2015, 11:54
par Amandinefch » 25 Oct 2015, 11:54
Oui mais n'ayant jamais vu f'' en cours, je ne peux pas utiliser ceci dans mon DM.
J'ai oublié de préciser que je viens d'un bac ST2S et que je suis actuellement en deuxième année de BTS Optique Lunetterie.
Je vous remercie tout de même pour vos réponses.
-
Amandinefch
- Messages: 7
- Enregistré le: 25 Oct 2015, 11:14
-
 par Amandinefch » 25 Oct 2015, 11:56
par Amandinefch » 25 Oct 2015, 11:56
f'0 = 0
2 * e^(2*0) - 2 = 2 * 1 -2 = 0
-
mathelot
 par mathelot » 25 Oct 2015, 12:00
par mathelot » 25 Oct 2015, 12:00
mathelot a écrit:une petite astuce
=2e^{2x}-2)
puis calcule f''
Le signe de f'' te permet de remonter aux variations de f.
excuse moi, le recours à
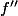
n'est pas nécessaire. Il est clair que
=0)
et

est strictement croissante sur R
donc

sur
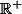
et

sur
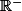
-
Amandinefch
- Messages: 7
- Enregistré le: 25 Oct 2015, 11:14
-
 par Amandinefch » 25 Oct 2015, 12:05
par Amandinefch » 25 Oct 2015, 12:05
C'est bien beau d'avoir trouver la variation de f', sauf qu'il me faut celle de f en passant par f' . ;) Et il est dit dans mon DM que je dois mettre 2x en facteur mais comment est-ce possible ayant exp^(2x) - 2x - 1 ? Pour moi c'est impossible ! Non ? ;)
-
Amandinefch
- Messages: 7
- Enregistré le: 25 Oct 2015, 11:14
-
 par Amandinefch » 25 Oct 2015, 12:10
par Amandinefch » 25 Oct 2015, 12:10
Ou alors je ne suis pas les conseilles de mon prof et je factorise la dérivée par 2, ce qui donnerais :
f'(x) = 2 (exp^(2x) - 1)
-
mathelot
 par mathelot » 25 Oct 2015, 12:16
par mathelot » 25 Oct 2015, 12:16
la variation de f' donne le signe de f'.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 25 Oct 2015, 14:30
par Carpate » 25 Oct 2015, 14:30
mathelot a écrit: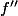
est la dérivée de

.
Ici,
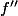
est trivialement strictement positive donc f' est croissante strictement.
Que vaut
)
?
@ Amandinefch
je ne vois pas l'intérêt de calculer f''(x) pour avoir le signe de f'(x)
 =2(e^{2x} -e^0))
la fonction exponentielle étant monotone, croissante sur R,

est du signe de

soit de

donc f décroissante sur

, croissante sur

et présente un minimum nul en 0
Edit : Pardon pour ce doublon tardif avec Mathelot !
-
Amandinefch
- Messages: 7
- Enregistré le: 25 Oct 2015, 11:14
-
 par Amandinefch » 25 Oct 2015, 14:36
par Amandinefch » 25 Oct 2015, 14:36
C'est ce que j'ai finalement fait ! Mais merci pour cette réponse même tardive ! :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
est la dérivée de
.
est trivialement strictement positive donc f' est croissante strictement.
?
