Petit soucis avec un changement de variable

[Flo38]

bonjour

tout d'abord je vous explique un peu le contexte

on a fait en cours il n'y a pas tres longtemps le changement de variable des intégrales

pour l'instant on en est en gros à :

on a une intégrale, on nous donne la fonction notée Phy (le changement de variable) et on passe d'une intégrale à l'autre en appliquant le théoreme..

en gros on ne comprend pas réellement comment choisir le changement de variable,et on se mélange vite des qu'on change de noms pour les variables..

selon le théoreme on passe d'une intégrale à l'autre comme ceci :

Int(a,b)Phy'(x)f(phy(x))dx=A=Int(Phy(a),Phy(b))f(t)dt=B

les hypothèses étant f C0 sur I, Phy C1 sur J à valeur dans I

j'ai eu cette aprem en colle l'exercice suivant :

on à f C0, et f(x)=f(a+b-x) (on m'a dit le nom je me rappelle plus..)

démontrer que Int(a,b)xf(x)=(a+b)/2Int(a,b)f(x)dx

après avoir cherché un peu par IPP etc, le gars m'a éclairé en me disant de poser u=a+b-x un changement de variable..

bon ok, déjà pas compris pourquoi mais on va tenter de le faire..

et là, gros gros soucis, pas foutu de savoir si on partait du cas A ou du cas B (donc problème pour changer les bornes..)

moi je partais sur :

Int(a,b)x(fx))dx=Int(bornes à trouver)(a+b-u)f(a+b-u)(-du)

en gros je remplace x par sa valeur et dx aussi..

et là pour trouver les bornes il me dit à la fin de mettre Phy(a) et Phy(b)

mais pourquoi ? voyez vous vraiment la forme A dans mon intégrale d'où je pars ? j'ai vraiment l'impression d'etre dans une B...d'ailleur apres mon premier changement maintenant je vois plutot une forme A..., donc bien un passage de B à A)

merci de m'aider ça m'embete un peu..et je suis sur que c'est tout con..

[fatal_error]

Salut,

en fait si tu as
u=a+b-x , tu dérives de chaque coté par rapport aux variables :
du=0 + 0 -dx
stout.

Pour les bornes,
si tu as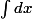 alors les bornes sont fonctions de x.
Si tu veux une integrale type alors les bornes sont fonctions de u.
Tu cherches tout simplement la valeur de u quand x vaut resp sa valeur minimale ()et maximale ().
Cad x=3, tu as u=1+b-3
De même x=22, u=a+b-22

Concernernant l'intégrale,
tu as donc

[Flo38]

mais du coup comme tu me l'explique, tu ne te préoccupe plus du théoreme..avec une astuce je vois bien pourquoi il faut faire le changement comme ça, c'est vis à vis du théoreme que je ne comprends pas..

[fatal_error]

la, comme ca, je serais incapable de te démontrer le théorême, désolé :(

[Flo38]

je demande pas une démo du théoreme hein !

ça je sais faire, très simple même

mais c'est dans ce cas particulier que je me rends compte que je n'ai pas si bien compris que ça..

c'est vrai qu'une fois connaissant le changement de variable on voit souvent très bien par rapport à la fonction, si on est sous le type A ou B du théorème, alors après on fait le changement de variable et on sait adapter les bornes selon si on est passé de B à A ou A ou B..

et là j'avoue que je ne reconnais pas du tout la forme de départ..

[fatal_error]

D'apres ce que je comprends tu voudrais savoir si on se trouve au départ avec une intégrale de type B ou A
est de type B: on peut poser x=cos(t)
En fait, on remarque qu'on peut "isoler" x.ici, on aurait \phi(t)=cos(t)=x

Mais des fois, on pose une variable 'égale' à une fonction :
ou on pose 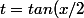, ici, on voit que les bornes de t vont dépendre de x, donc on se trouve dans le cas A.(\phi(x)=t)

Dans ton cas, tu as .
Si tu poses u=a+b-x, tu vois bien que tu es initialement dans le cas a, vu que u va dépendre des bornes de x (u=\phi(x))

Enfin, je pense, et de manière générale que on place le \phi, la ou la variable n'est pas isolée, comme ca je suis sûr d'avoir dit au moins une connerie :happy2:

[fatal_error]

lol, du coup je viens de me rendre compte que moi non plus :D.

Mais bon, ca ne change pas grand chose, le changement de variable se fait si ya bijection, donc si tu as
x=f(t) tu as aussi t=f^{-1}(x)
cad dx=f('t)dt ou dt=(f^{-1})'(x) dx
Donc dans les deux cas on peut prétendre à une forme \phi.

après savoir dans quel cas on se trouve, je sais pas, j'aurais du me poser la question.Peut-être. :cry: