Somme de série avec intégrales de Wallis

[tetraedre]

Quelqu’un peut il m’aider à calculer la somme suivante dans laquelle wk est une intégrale de Wallis :

[issoram]

Bonsoir,

Il y a plusieurs façons d'aborder la chose. Dans quel cadre cette question t'es posée? As-tu démontré des résultats intermédiaires avant cette question?

[mathelot]

Quelqu’un peut il m’aider à calculer la somme suivante dans laquelle wk est une intégrale de Wallis :

Les notations sont mauvaises. La lette x est réservée à la somme des x^k.
La variable d'intégration est muette, on peut la changer mais sans prendre la notation cos(x)^k dx
la variable x étant déja prise.

je te propose donc:

[tetraedre]

bonjour

La variable d'intégration est bien x...

Dans un premier exercice, x^k est remplacé par (-1)^k.

Il faut montrer que l'on peut intervertir les signes somme et intégrale :



Puis le calcul de la somme est simple : on a une progression géométrique de raison q = -cos(x) dont on sait calculer la somme.

Mais dans le second exercice, on ne peut pas intervertir les signes somme et intégrale ...et donc je coince !
Il faut peut être faire des changements de variables et utiliser les propriétés des intégrales de Wallis .

[mathelot]

bonjour

La variable d'intégration est bien x...

non.
si tu prend x pour variable d'intégration au lieu de u , tu ne peux pas faire rentrer le x^k à l'intérieur de l'intégrale.

[issoram]

Bonjour,

Il faut bien que tu distingues, comme te l'a dit Mathelot, ta variable d'intégration (muette) et ta variable de sommation. Ceci étant dit, en posant:


et


1) Il faut d'abord (si pas fait dans une question précédente) que tu détermines le rayon de convergence de la série entière de terme général .

2) Ceci fait, pour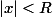 , tu pourras calculer la somme , en intervertissant somme et intégrale. (à toi de préciser pourquoi c'est possible dans ce cas...)

3) L'intégrale que tu obtiens pour , se calcule alors par changements de variables.

[tetraedre]

merci pour votre aide précieuse !

Effectivement en prenant t comme variable d'intégration , en considérant un rayon de convergence R=1 ( rapport de In+1 / in ) et en justifiant l'échange des signes somme et intégrale , on retombe sur une progression géométrique de raison q = xcos(t). Au final il reste l'intégrale ci-dessous à calculer...

[mathelot]

bonsoir,



On pose avec



soit:

[tetraedre]

Je suis d'accord avec ce résultat .

A noter que le résultat pour la somme similaire ci-dessous est surprenant puisqu'on trouve S(x)=1 !

[issoram]

Pour être plus précis on trouve

Tu peux te poser la question de savoir si ce résultat colle avec l'expression de S(x) donnée par Mathelot.

Qu'en conclure?

[tetraedre]

Cela revient à calculer :



C'est ce résultat que je trouve étonnant..

[mathelot]

Quand x tend vers -1+:




d'où

[tetraedre]

On a donc montré que les deux séries ont la même somme .....