Somme de cos(k*téta)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Oct 2006, 18:14
par skyskiper » 09 Oct 2006, 18:14
Re-salut! J'ai de nouveau besoin d'aide, mais pour de la trigo cette fois-ci!
J'ai beau chercher toutes les méthodes possibles et essayer toutes les formules de trigo que je connais, je n'arrive pas à trouver le réultat que l'on me demande... Si quelqu'un peut m'aider...?
Voilà ce qu'on me demande de démontrer:
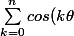=\frac{1-cos((n+1)\theta)-cos(\theta)+cos(n\theta)}{2(1-cos(\theta))})
En attendant, merci à tous ceux qui prendront un peu de leur temps pour me répondre!
++ :ptdr:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Oct 2006, 18:31
par Zebulon » 09 Oct 2006, 18:31
Bonsoir,
je pense qu'il suffit d'utiliser que pour tout entier k,
=Re(e^{ki\theta}))
.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Oct 2006, 18:47
par Zebulon » 09 Oct 2006, 18:47
Ce n'est pas plutôt :
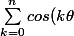=\frac{1-cos((n-1)\theta)-cos(\theta)-cos(n\theta)}{2(1-cos(\theta))})
avec
\theta))
et
})
?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Oct 2006, 19:44
par Flodelarab » 09 Oct 2006, 19:44
moi je trouve tout bon avec une bonne vieille récurrence et le développement de cos(a)cos(b)
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Oct 2006, 20:08
par skyskiper » 09 Oct 2006, 20:08
Zebulon a écrit:Ce n'est pas plutôt :
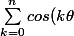=\frac{1-cos((n-1)\theta)-cos(\theta)-cos(n\theta)}{2(1-cos(\theta))})
avec
\theta))
et
})
?
Désolé mais c'est bien l'expression que j'ai écrite...
Je vais essayer par récurence mais le développement me semble assez long...
Je vous tiens au courant. Merci pour votre aide!
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Oct 2006, 20:10
par Zebulon » 09 Oct 2006, 20:10
Je pense que ma méthode marche bien mais que j'ai fait une erreur de calcul. :hum:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Oct 2006, 20:12
par Flodelarab » 09 Oct 2006, 20:12
skyskiper a écrit:Désolé mais c'est bien l'expression que j'ai écrite...
Je vais essayer par récurence mais le développement me semble assez long...
Je vous tiens au courant. Merci pour votre aide!
ça fait peur mais tu verras que ça se simplifie très très vite

-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Oct 2006, 20:25
par skyskiper » 09 Oct 2006, 20:25
Le méthode de récurence fonctionne très bien!
Mais vu que j'aime beaucoup me casser la tête, je vais aussi faire la méthode de Zebulon! lol
Je vous tiens au courant!
Merci pour votre aide!
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Oct 2006, 20:29
par skyskiper » 09 Oct 2006, 20:29
Heu... peux-tu me donner le début de ton calcul Zebulon parce que je ne sais même pas par où commencer...lol
++
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Oct 2006, 20:39
par Zebulon » 09 Oct 2006, 20:39
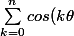}=<br />\sum\limits_{k=0}^n{Re}(e^{ki\theta})=<br />Re(\sum\limits_{k=0}^n{e^{ki\theta}})=<br />Re(\sum\limits_{k=0}^n{(e^{i\theta})^k})=...?)
Moi, j'ai la flemme de refaire le calcul...
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Oct 2006, 20:44
par skyskiper » 09 Oct 2006, 20:44
Bah c'est pas grave, je n'ai plus trop le temps de regarder ta méthode, encore pas mal de boulo... :briques: lol
Mais à l'occaz!
En tout cas, merci à vous deux!
++
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Oct 2006, 20:48
par Zebulon » 09 Oct 2006, 20:48
J'ai trouvé mon erreur! J'avais écrit n au lieu de n+1.
Si tu restes encore un peu, j'écris la calcul.
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Oct 2006, 20:55
par skyskiper » 09 Oct 2006, 20:55
Ok je reste pour voir comment tu fais alors!
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Oct 2006, 21:13
par Zebulon » 09 Oct 2006, 21:13
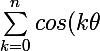}=<br />\sum\limits_{k=0}^n{Re}(e^{ki\theta})\\=<br />Re(\sum\limits_{k=0}^n{e^{ki\theta}})=<br />Re(\sum\limits_{k=0}^n{(e^{i\theta})^k})\\=<br />Re\bigg({{{1-(e^i\theta})^{n+1}}\over{1-e^{i\theta}}}\bigg)=<br />Re\bigg({{1-cos((n+1)\theta)-isin((n+1)\theta)}\over{1-cos(\theta)-isin(\theta)}}\bigg)\\=<br />Re\bigg({\big[{1-cos((n+1)\theta)-isin((n+1)\theta)\big]\big[1-cos(\theta)+isin(\theta)\big]}\over{(1-cos(\theta))^2+sin^2(\theta)}}\bigg)<br />\\={{1-cos(\theta)-cos((n+1)\theta)+cos(\theta)cos((n+1)\theta)+sin({\theta})sin((n+1)\theta)}\over{1-2cos(\theta)+cos^2(\theta)+sin^2(\theta)}})
Or
=cos(a)cos(b)+sin(a)sin(b))
donc
=cos((n+1)\theta-\theta)=cos(\theta)cos((n+1)\theta)+sin({\theta})sin((n+1)\theta))
donc
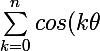}={{1-cos(\theta)-cos((n+1)\theta)+cos(n\theta)}\over{2-2cos(\theta)}})
.
Pfouuuu...
A+ :++:
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Oct 2006, 21:24
par skyskiper » 09 Oct 2006, 21:24
Zebulon a écrit: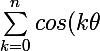}=<br />\sum\limits_{k=0}^n{Re}(e^{ki\theta})\\=<br />Re(\sum\limits_{k=0}^n{e^{ki\theta}})=<br />Re(\sum\limits_{k=0}^n{(e^{i\theta})^k})\\=<br />Re\bigg({{{1-(e^i\theta})^{n+1}}\over{1-e^{i\theta}}}\bigg)=<br />Re\bigg({{1-cos((n+1)\theta)-isin((n+1)\theta)}\over{1-cos(\theta)-isin(\theta)}}\bigg)\\=<br />Re\bigg({\big[{1-cos((n+1)\theta)-isin((n+1)\theta)\big]\big[1-cos(\theta)+isin(\theta)\big]}\over{(1-cos(\theta))^2+sin^2(\theta)}}\bigg)<br />\\={{1-cos(\theta)-cos((n+1)\theta)+cos(\theta)cos((n+1)\theta)+sin({\theta})sin((n+1)\theta)}\over{1-2cos(\theta)+cos^2(\theta)+sin^2(\theta)}})
Or
=cos(a)cos(b)+sin(a)sin(b))
donc
=cos((n+1)\theta-\theta)=cos(\theta)cos((n+1)\theta)+sin({\theta})sin((n+1)\theta))
donc
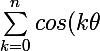}={{1-cos(\theta)-cos((n+1)\theta)+cos(n\theta)}\over{2-2cos(\theta)}})
.
Pfouuuu...
A+ :++:
Ok, je vois.... la méthode par récurence est un peu plus longue mais plus simple je pense, lol! Enfin en tout cas, c'est un beau calcul! (mais je ne me sens pas encore capable de le mener seul à bien! lol)
++ et merci à toi! :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 10 Oct 2006, 06:36
par Zebulon » 10 Oct 2006, 06:36
En utilisant la même démonstration, je trouve la formule analogue avec le sinus :
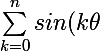}={{sin({\th})-sin((n+1)\theta)+sin(n\theta)}\over{2(1-cos(\theta))}})
si je ne me suis pas trompée...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
