Bonjour, je suis en train de traiter un exercice qui peut sembler simple mais qui me pose des difficultés, la consigne est en PJ (par faute de clarté si je l'écris ici).
J'ai repéré les identités remarquables en dénominateur, mais je ne sais pas quoi en faire après; j'ai essayé moultes solutions (réduction au même dénominateur, développement et factorisation...) mais aucune ne semble me mener à une expression plus simple que celle de départ.
À moins que la simplification consiste à simplement faire apparaître les identités remarquables, je ne sais pas résoudre ce problème.
Quelqu'un pourrait-il m'indiquer une méthode qui me permettant d'aboutir au résultat "simplifié"?
Merci beaucoup pour votre temps, je m'excuse de la gêne occasionnée.
Simplification de fraction
4 messages
- Page 1 sur 1
Simplification de fraction
He who asks a question is a fool for five minutes; he who does not ask a question remains a fool forever.
Re: Simplification de fraction
Bonjour,
P.S. : ça veux dire quoi PJ?
nous ne voyons rien, donc impossible de t'aider
tu as 2 possibilités:
1) passer par un hébergeur d'image
2) ou recopier ce qui manque
.... la consigne est en PJ (par faute de clarté si je l'écris ici).
P.S. : ça veux dire quoi PJ?
nous ne voyons rien, donc impossible de t'aider
tu as 2 possibilités:
1) passer par un hébergeur d'image
2) ou recopier ce qui manque
Re: Simplification de fraction
Bonjour, PJ signifie pièce jointe. En effet le fichier joint n'est apparemment pas disponible.
Voici l'énoncé (en espérant que ce soit assez clair):
Simplifier (il s'agit bien de 2 puissance 2^n):
(1/((2^(2^n)) -1) - (1/((2^2^(n+1))-1)
(https://cdn.discordapp.com/attachments/ ... nknown.png ; voici un lien qui mène à une image de l'énoncé)
Je suis désolé pour la confusion que peuvent susciter mes messages, c'est la première fois que je poste sur ce forum
Bien à vous.
Voici l'énoncé (en espérant que ce soit assez clair):
Simplifier (il s'agit bien de 2 puissance 2^n):
(1/((2^(2^n)) -1) - (1/((2^2^(n+1))-1)
(https://cdn.discordapp.com/attachments/ ... nknown.png ; voici un lien qui mène à une image de l'énoncé)
Je suis désolé pour la confusion que peuvent susciter mes messages, c'est la première fois que je poste sur ce forum

Bien à vous.
He who asks a question is a fool for five minutes; he who does not ask a question remains a fool forever.
Re: Simplification de fraction
Bonjour
En fait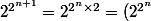^2)
Donc c'est comme si on avait 1/(a-1)-1(a²-1) ce qui n'est pas difficile à traiter.
En fait
Donc c'est comme si on avait 1/(a-1)-1(a²-1) ce qui n'est pas difficile à traiter.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
