Séries de Fourier
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Jota
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Nov 2018, 04:26
-
 par Jota » 10 Fév 2019, 00:43
par Jota » 10 Fév 2019, 00:43
Salut,
On me demande de montrer que
\frac{t}{2})}{\sin(\frac{t}{2})}dt}=\pi , \forall n\in \mathbb{N})
en utilisant la formule de Dirichlet.
Merci d'avance.
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
 par FLBP » 10 Fév 2019, 02:02
par FLBP » 10 Fév 2019, 02:02
-
aviateur
 par aviateur » 10 Fév 2019, 10:58
par aviateur » 10 Fév 2019, 10:58
Bonjour
Ce que tu appelles la formule de Dirichlet consiste surement en la linéarisation de
=\dfrac{\sin((2n+1)t/2)}{\sin (t/2)})
et puis intégrer termes à termes.
Le plus simple pour toi c'est de calculer
-f_{n-1}(t))
en appliquant la formule sin(a+b) ....
Pour trouver
-f_{n-1}(t)=2 \cos(n t).)
Dont l'intégrale est nulle pour

Ce qui montre que l'intégrale ne dépend pas de n. Il suffit alors de faire le calcul pour n=0 pour trouver

.
-
Jota
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Nov 2018, 04:26
-
 par Jota » 10 Fév 2019, 20:33
par Jota » 10 Fév 2019, 20:33
Salut, en fait voici ce que dit le lemme dans notre cours.
Soit

la fonction 2

- périodique et Riemann integrable sur [0, 2

[.
La suite des sommes partielles
_{n})
associé à la série de Fourier de f vérifie pour tous
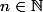
et
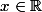
,
=\frac{1}{2\pi}\int_{0}^{2\pi}{<br /> \frac{\sin((2n+1)\frac t2)}{\sin\frac t2}(f(x+t)+f(x-t))dt})
.
-
aviateur
 par aviateur » 10 Fév 2019, 20:39
par aviateur » 10 Fév 2019, 20:39
Oui mais c'est pas la question. On te demande de calculer l'intégrale avec la "formule de Dirichlet".
Donc je te donne la démonstration qui donne la formule de Dirichlet ou ce qui revient au même comment calculer l'intégrale, parce que quiconque voudra calculer cette intégrale, pensera à linéariser et non pas à utiliser le théorème de Dirichlet.
-
Jota
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Nov 2018, 04:26
-
 par Jota » 10 Fév 2019, 20:50
par Jota » 10 Fév 2019, 20:50
Je ne comprends pas bien ton raisonnement.
-
aviateur
 par aviateur » 11 Fév 2019, 09:52
par aviateur » 11 Fév 2019, 09:52
Mon raisonnement consiste à retrouver la formule de Dirichlet et de montrer que l'intégrale vaut

As tu calculé
-f_n(t))
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités