Séries de Fourier
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
M07
- Messages: 2
- Enregistré le: 08 Mai 2010, 15:11
-
par M07 » 08 Mai 2010, 15:25
Bonjour à tous,
Un problème m'est survenu en voulant trouvé les coefficient de fourriers d'une fonction.
Cela doit être tout bête mais je dois reconnaitre qu'en ayant chercher plusieurs heures, je ne suis pas parvenu à résoudre ce problème.
- Code: Tout sélectionner
f(x) = x^(2m) x appartient à l'intervalle (-Pi, Pi) et m appartient à N
pour a0 et c0 j'ai trouvé:
a0 = (Pi^(2m))/(2m+1)
Donc pour ca pas de souci mais pour aN ou cN je n'arrive pas à les trouver.
- Code: Tout sélectionner
an = 2/PI * Integral (de 0 à Pi) de (f(x)*cos(nx) dx)
Et donc pour calculer cette intégrale j'ai eu la fausse idée de faire une intégration par partie. Comme m est inconnu, je ne peux pas faire m intégration par partie.
Donc ma question est la suivante:
Comment faire pour trouver an ou cn?
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 08 Mai 2010, 17:07
Salut,
L'idée de faire m intégrations par parties est la bonne.
En fait, comme on ne connait pas m, on fait une seule intégration par partie puis une réccurence (tu as intérêt à calculer plutôt cn, sinon il y a un problème de parité...)
Pour être plus précis,
tu fixe un
, puis, pour tout m dans
, tu pose
.
Tu calcule
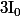
et, pour
, tu établit une relation de récurrence entre
et
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
M07
- Messages: 2
- Enregistré le: 08 Mai 2010, 15:11
-
par M07 » 08 Mai 2010, 18:16
Merci pour ta réponse, j'ai compris la méthode que je connaissais et que j'avais oublié :cry: . Je ne suis quand même pas arriver à trouver la solution.
J'ai intégré deux fois par partie Im pour trouver tant bien que mal Im-1. Mais bon vu la tête de la correction, je suis loin du compte :triste: .
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 08 Mai 2010, 19:23
Soit
fixé et, pour tout m dans
,
.
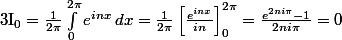
Pour
, on a :
^{2m}}{2n i\pi}<br />-\frac{2m}{2n i\pi}\int_{0}^{2\pi}x^{2m-1}e^{inx}\,dx)
^{2m-1}}{n i}<br />-\frac{m}{n i\pi}\left[\frac{e^{inx}}{i n}x^{2m-1}\right]_{0}^{2\pi}<br />+\frac{m}{n i\pi}\int_{0}^{2\pi}(2m-1)x^{2m-2}\,\frac{e^{inx}}{i n}\,dx)
^{2m-1}}{n i}<br />+\frac{2m(2\pi)^{2m-2}}{n^2}<br />-\frac{2m(2m-1)}{n^2}I_{m-1})
Donc (réccurence)
^{2m-1}}{n i}<br />+\frac{2m(2\pi)^{2m-2}}{n^2}<br />-\frac{2m(2m-1)(2\pi)^{2m-3}}{n^3 i}<br />-\frac{2m(2m-1)(2m-2)(2\pi)^{2m-4}}{n^4}<br />+\cdots<br />+(-1)^{m-1}\frac{2m(2m-1)...3(2\pi)^1}{n^{2m-1} i}<br />+(-1)^{m-1}\frac{2m(2m-1)...2(2\pi)^0}{n^{2m}})
C'est à dire
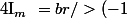^{m-1}\,\frac{(2m)!}{n^{2m}}\,\bigsum_{k=0}^{2m-1}<br />\frac{1}{(k+1)!}(-2ni\pi)^k)
Que je ne pense pas que l'on puisse simplifier...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 109 invités
