Série?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 07:27
par youyou2 » 18 Oct 2009, 07:27
Bonjour à tous,
Un= (-1)^n / (n²+(-1)^(n+1)), monter que cette série est absolument convergente
Merci d'avance :hein:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 18 Oct 2009, 07:30
par fatal_error » 18 Oct 2009, 07:30
salut,
c'est quoi une série absolument convergente?
la vie est une fête

-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 07:33
par youyou2 » 18 Oct 2009, 07:33
Franchement, je me suis posé la même question!!!
Je suppose que c'est juste pour dire convergente mais c'est pas sûr!!!
Dans l'exercice, c'est précisé que (c'est à dire que la série de terme général
lUnl est convergente)
lUnl >>> valeur absolue
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 07:56
par youyou2 » 18 Oct 2009, 07:56
personne sur les suites?! :cry:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 18 Oct 2009, 07:59
par fatal_error » 18 Oct 2009, 07:59
ben donc c'est pas la même chose.
Par exemple :
pour
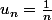
^n}{n})
est convergente, mais
^n}{n}|)
est pas convergente, cad
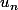
n'est pas absolument convergente.
Tu peux commencer par remplacer u_n par |u_n| dans ton exo et voir ce que ca entraine.
la vie est une fête

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Oct 2009, 07:59
par girdav » 18 Oct 2009, 07:59
Donc, que vaut

?
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 08:10
par youyou2 » 18 Oct 2009, 08:10
fatal_error a écrit:ben donc c'est pas la même chose.
Par exemple :
pour
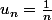
^n}{n})
est convergente, mais
^n}{n}|)
est pas convergente, cad
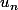
n'est pas absolument convergente.
Tu peux commencer par remplacer u_n par |u_n| dans ton exo et voir ce que ca entraine.
Pour moi,
^n}{n})
diverge! c'est une série de Reimann ca non?!

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 18 Oct 2009, 08:21
par fatal_error » 18 Oct 2009, 08:21
les séries de riemann sont de la forme :

dapres wiki.
Tu vois que le
^n)
est "en plus" donc c'est pas une serie de riemann. Il s'avère que c'est une serie qui converge avec le theoreme des series alternées.
Bref, tout ca pour dire que convergence (simple) et convergence absolues c'est pas pareil.
CVA => CVS, mais non(CVA) nimplique pas non(CVS)
la vie est une fête

-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 08:34
par youyou2 » 18 Oct 2009, 08:34
Ok, dans mon cour, on les appel série harmonique alternée!
^n}{n}|)
est pas convergente, cad
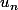
n'est pas absolument convergente.
Par contre je ne comprend pas pourquoi en valeur absolue, n'est pas convergente?!

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 18 Oct 2009, 08:51
par fatal_error » 18 Oct 2009, 08:51
la série

diverge. C'est une serie de "référence". Voir la constante d'euler sur wikipedia
Edit, comme tu as vu les series de riemann, tu dois aussi savoir que

ne converge que pour

la vie est une fête

-
Black Jack
 par Black Jack » 18 Oct 2009, 09:08
par Black Jack » 18 Oct 2009, 09:08
fatal_error a écrit:salut,
c'est quoi une série absolument convergente?
Pour info :
Une série de terme général Un est dite absolument convergente si la suite de terme général |Un| est convergente.
:zen:
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 09:28
par youyou2 » 18 Oct 2009, 09:28
fatal_error a écrit:la série

diverge. C'est une serie de "référence". Voir la constante d'euler sur wikipedia
Edit, comme tu as vu les series de riemann, tu dois aussi savoir que

ne converge que pour

Donc (-1)^n / (n² + (-1)^(n+1) ) devient en valeur absolue 1/n²?! non?
et comme {\alpha}}>1 donc la série est absolument convergente?!
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Oct 2009, 09:30
par girdav » 18 Oct 2009, 09:30
Attention au dénominateur! (même si ce qui manque ne joue aucun rôle du point de vue de la convergence )
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 09:32
par youyou2 » 18 Oct 2009, 09:32
girdav a écrit:Attention au dénominateur! (même si ce qui manque ne joue aucun rôle du point de vue de la convergence )
On peut le négliger!
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Oct 2009, 09:54
par girdav » 18 Oct 2009, 09:54
Ce n'est donc pas égal mais équivalent au voisinage de

.
-
youyou2
- Membre Naturel
- Messages: 64
- Enregistré le: 14 Déc 2008, 16:06
-
 par youyou2 » 18 Oct 2009, 09:55
par youyou2 » 18 Oct 2009, 09:55
girdav a écrit:Ce n'est donc pas égal mais équivalent au voisinage de

.
Ok précision utile!!! merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
 dapres wiki.
dapres wiki.^n) est "en plus" donc c'est pas une serie de riemann. Il s'avère que c'est une serie qui converge avec le theoreme des series alternées.
est "en plus" donc c'est pas une serie de riemann. Il s'avère que c'est une serie qui converge avec le theoreme des series alternées.
diverge. C'est une serie de "référence". Voir la constante d'euler sur wikipedia
ne converge que pour
