Bonjour à tous,
Il s'agit de calculs matriciels avec des vecteurs. Je me souviens comment procéder pour calculer les nouvelles coordonnées d'un vecteur suite à une rotation autour d'un vecteur quelconque.
Le problème est que je me demande comment connaître les valeurs angulaires de cette rotation avec une combinaison de deux vecteurs connus. Comment calculer ces valeurs angulaires ?
Pouvez-vous m'aiguiller ?
Merci.
Rotation dans R3
9 messages
- Page 1 sur 1
Re: Rotation dans R3
Salut,
J'ai pas tout capté...
Tu connait deux vecteurs U et V de R^3 ainsi que leurs images U' et V' par une certaine rotation R inconnue et tu aimerais en déduire l'angle (et éventuellement l'axe) de la rotation R ?
C'est ça ou je suis complètement à coté de la plaque ?
J'ai pas tout capté...
Tu connait deux vecteurs U et V de R^3 ainsi que leurs images U' et V' par une certaine rotation R inconnue et tu aimerais en déduire l'angle (et éventuellement l'axe) de la rotation R ?
C'est ça ou je suis complètement à coté de la plaque ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Rotation dans R3
salut ben
je pense que MacErmite2 veut à partir de deux vecteurs 3D, connaitre l'angle entre ces deux vecteurs.
si on nomme u et v ces deux vecteurs, et w = u vect v, ya une rotation de u à v d'axe w (en translatant au besoin v jusqu'à ce que la base de u et v soit la même), et MacErmite2 veut connaitre la valeur de cet angle.
j'aurais pour ma part tendance (moyennant que l'interpretation soit bonne) à simplement prendre le produit scalaire des normés puis acos vu que je vois pas trop comment définir l'orientation...
je pense que MacErmite2 veut à partir de deux vecteurs 3D, connaitre l'angle entre ces deux vecteurs.
si on nomme u et v ces deux vecteurs, et w = u vect v, ya une rotation de u à v d'axe w (en translatant au besoin v jusqu'à ce que la base de u et v soit la même), et MacErmite2 veut connaitre la valeur de cet angle.
j'aurais pour ma part tendance (moyennant que l'interpretation soit bonne) à simplement prendre le produit scalaire des normés puis acos vu que je vois pas trop comment définir l'orientation...
la vie est une fête 
Re: Rotation dans R3
Il y a l'image U' de U , qui est le résultat d'une rotation autour du vecteur D d'angle Theta.
Je cherche alors , compte tenu de l'image U' défini à présent, à exprimer les rotations autour du vecteur A d'angle Beta et le vecteur B d'angle Gamma.
U' est alors le résultat d'une rotation autour du vecteur A d'angle Beta , puis d'une rotation autour du vecteur B d'angle Gamma.
Je cherche alors , compte tenu de l'image U' défini à présent, à exprimer les rotations autour du vecteur A d'angle Beta et le vecteur B d'angle Gamma.
U' est alors le résultat d'une rotation autour du vecteur A d'angle Beta , puis d'une rotation autour du vecteur B d'angle Gamma.
Re: Rotation dans R3
Bon, ben... je comprend rien...MacErmite2 a écrit:Il y a l'image U' de U , qui est le résultat d'une rotation autour du vecteur D d'angle Theta.
Je cherche alors , compte tenu de l'image U' défini à présent, à exprimer les rotations autour du vecteur A d'angle Beta et le vecteur B d'angle Gamma.
U' est alors le résultat d'une rotation autour du vecteur A d'angle Beta , puis d'une rotation autour du vecteur B d'angle Gamma.
Déjà et pour commencer, si tu connait deux vecteurs U et U' alors
- Soit ils ont pas la même norme et il n'existe pas de rotations R telles que R(U)=U'.
- Soit ils ont même normes et il y a une infinité de rotations R telles que R(U)=U' donc ils ne permettent pas de caractériser un axe (dirigé par D) ni un angle Theta.
Ensuite, je vois absolument pas le rapport entre cette première phrase et la suivante parlant de point A et B et d'angles alpha et gamma (donc rien en commun avec la première phrase)
Et c'est encore pire avec la dernière phrase et son "U' défini à présent" qui me semble complètement contraire à la première phrase où on considérait que U et U' étaient connu dés le début.
Te serait il possible de dire précisément :
- Quels sont les objets (vecteurs, angles, rotations,...) connus au départ ?
- Quels sont les objets (vecteurs, angles, rotations,...) qu'on cherche à déterminer ?
- Quels liens il doit y avoir entre les objets "connus" et ceux "à déterminer" ?
Enfin bref, d'écrire un truc compréhensible du style :
On se donne au départ . . . . . et on cherche à déterminer . . . . tels que . . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Rotation dans R3
MacErmite2 a écrit:Il y a l'image U' de U , qui est le résultat d'une rotation autour du vecteur D d'angle thêta.
Soit R1 la matrice de rotation d'angle thêta, autour du vecteur D et un vecteur U.
Soit l'opération suivante : U' = R1.U
Données d'entrée : R1, thêta, D et U.
Je cherche alors , compte tenu de l'image U' défini à présent, à exprimer les rotations autour du vecteur A d'angle bêta et le vecteur B d'angle Gamma
Soit deux vecteurs A et B. Je cherche à exprimer R2 et R3, avec R2 la matrice de rotation d'angle bêta, autour du vecteur A et R3 la matrice de rotation d'angle gamma, autour du vecteur B.
Données d'entrée : A, B.
Inconnues : R2, R3, bêta, gamma.
U' est alors le résultat d'une rotation autour du vecteur A d'angle bêta , puis d'une rotation autour du vecteur B d'angle Gamma.
U'' = R2.U puis U'=R3.U''
U'' est alors l'image de U par la rotation de U d'un angle bêta autour du vecteur A, puis rotation de U'' d'un angle gamma autour du vecteur B
Expressions de R1 et R2 ? (cela revient à rechercher les valeurs de bêta et gamma.)
En espérant avoir été plus claire.
Re: Rotation dans R3
Si je comprend bien :
Au départ sont connus 4 vecteurs U , U' , A , B qu'on peut supposer unitaires :
- Concernant les axes de rotation autour de A et B, ça ne change rien de les supposer unitaire.
- Concernant U, comme les rotations sont des applications linéaires, de le rendre unitaire va uniquement diviser ces images par la norme de U, mais ne rien changer aux différentes contraintes.
- Concernant U', il sera unitaire comme image de U par la rotation d'axe D d'angle thêta et vu la suite de l'énoncé, la connaissance de D et de thêta (c'est à dire de R1) n'apporte rien de bien utile comme information : ça permet uniquement de calculer U'.
Tu cherche alors à déterminer des angles et
et  (s'il en existe) tels que
(s'il en existe) tels que \big)\!=\!U') (où
(où  désigne la rotation d'axe
désigne la rotation d'axe  d'angle
d'angle 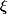 )
)
Si c'est bien ça alors déjà, un simple point de vue géométrique permet de voir qu'il peut ne pas y avoir de solutions et que, lorsqu'il y en a, il y en a en général deux (et exceptionnellement une seule) :
Lorsque décrit
décrit 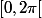 le vecteur
le vecteur ) décrit un cercle
décrit un cercle 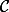 de la sphère unité (c'est l'intersection de la sphère unité et du plan perpendiculaire à
de la sphère unité (c'est l'intersection de la sphère unité et du plan perpendiculaire à  passant par
passant par  ) puis, lorsque
) puis, lorsque  décrit
décrit 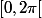 le vecteur
le vecteur \big)) décrit l'ensemble des images de
décrit l'ensemble des images de 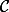 par les
par les  et on voit assez clairement ce qu'il se passe : seul une portion de la sphère délimitée par deux cercles parallèles (portés par des plans perpendiculaires à B) risque d'être décrite et tout les points strictement entre les deux cercles sont atteint deux fois.
et on voit assez clairement ce qu'il se passe : seul une portion de la sphère délimitée par deux cercles parallèles (portés par des plans perpendiculaires à B) risque d'être décrite et tout les points strictement entre les deux cercles sont atteint deux fois.
Donc si U' n'est pas dans cette portion de sphère, il n'y aura pas de solution et si U' est dans cette portion mais pas au bord (i.e. pas sur un des deux cercles), il y aura deux solutions.
Concernant le calcul explicite des deux couples) solutions du problème (lorsqu'ils existent) vu le point de vue géométrique (faire tourner un cercle suivant un axe quelconque) j'ai l'impression que ça va forcément être un peu compliqué.
solutions du problème (lorsqu'ils existent) vu le point de vue géométrique (faire tourner un cercle suivant un axe quelconque) j'ai l'impression que ça va forcément être un peu compliqué.
Perso., j'attaquerais sans doute par du calcul bourrin consistant à utiliser la définition calculatoire d'une rotation d'axe unitaire et d'angle
unitaire et d'angle 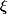 (*) :
(*) :
=\cos(\xi).V+\big(1-\cos(\xi)\big)\langle V|X\rangle.V+\sin(\xi).V\!\wedge\! X)
où désigne le produit scalaire de
désigne le produit scalaire de  et
et  et où
et où  désigne le produit vectoriel de
désigne le produit vectoriel de  et
et  .
.
Je peut éventuellement faire les calculs, mais vu la m... que ça va être, je préfèrerais être sûr avant que ça ça soit bien ça la problématique.
(*) Eventuellement, et si tu connait le concept, c'est plutôt plus simple à gérer en utilisant la formule calculatoire avec les quaternions.
Au départ sont connus 4 vecteurs U , U' , A , B qu'on peut supposer unitaires :
- Concernant les axes de rotation autour de A et B, ça ne change rien de les supposer unitaire.
- Concernant U, comme les rotations sont des applications linéaires, de le rendre unitaire va uniquement diviser ces images par la norme de U, mais ne rien changer aux différentes contraintes.
- Concernant U', il sera unitaire comme image de U par la rotation d'axe D d'angle thêta et vu la suite de l'énoncé, la connaissance de D et de thêta (c'est à dire de R1) n'apporte rien de bien utile comme information : ça permet uniquement de calculer U'.
Tu cherche alors à déterminer des angles
Si c'est bien ça alors déjà, un simple point de vue géométrique permet de voir qu'il peut ne pas y avoir de solutions et que, lorsqu'il y en a, il y en a en général deux (et exceptionnellement une seule) :
Lorsque
Donc si U' n'est pas dans cette portion de sphère, il n'y aura pas de solution et si U' est dans cette portion mais pas au bord (i.e. pas sur un des deux cercles), il y aura deux solutions.
Concernant le calcul explicite des deux couples
Perso., j'attaquerais sans doute par du calcul bourrin consistant à utiliser la définition calculatoire d'une rotation d'axe
où
Je peut éventuellement faire les calculs, mais vu la m... que ça va être, je préfèrerais être sûr avant que ça ça soit bien ça la problématique.
(*) Eventuellement, et si tu connait le concept, c'est plutôt plus simple à gérer en utilisant la formule calculatoire avec les quaternions.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Rotation dans R3
- Comme tu connais deux vecteurs, le produit vectoriel te donnera le 3ème vecteur. Ainsi tu obtiens la base associée à ton objet qui bouge après avoir tout normalisé.
- Avec les coordonnées des vecteurs de la base créée tu remplie ta matrice de passage "appelée P" de la base fixe à la base qui bouge.
-Ensuite tu considère une convention de Rotation par exemple X (theta1),Y' (theta2),Z" (theta3). Ceci donne trois matrices dont le produit donne une matrice de passage P' de la base fixe à la base qui bouge.
-Comme t'as deux expressions de la même matrice de passage, il suffit d'identifier P et P' et trouver les trois angles.
- Avec les coordonnées des vecteurs de la base créée tu remplie ta matrice de passage "appelée P" de la base fixe à la base qui bouge.
-Ensuite tu considère une convention de Rotation par exemple X (theta1),Y' (theta2),Z" (theta3). Ceci donne trois matrices dont le produit donne une matrice de passage P' de la base fixe à la base qui bouge.
-Comme t'as deux expressions de la même matrice de passage, il suffit d'identifier P et P' et trouver les trois angles.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
