Rotation dans le plan complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 08 Déc 2018, 18:21
par nix64 » 08 Déc 2018, 18:21
Bonjour
la démonstration de la proposition est brève je ne vois pas comment on a obtenu la forme complexe de la transformation c' est a dire commet z' = z0 + exp(i teta) (z-z0) avec teta est l angle de la rotation et z0 l' affixe de son centre

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Déc 2018, 19:07
par Carpate » 08 Déc 2018, 19:07
Appliquer une rotation d'angle

à un vecteur c'est multiplier son affixe par le complexe de module 1 et d'argument

soit
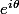

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 08 Déc 2018, 19:40
par nix64 » 08 Déc 2018, 19:40
oui je vois ça dans la démonstration mais d ou ça vien comment on traduit en terme de complexes a partir de la définition pour la translation et l homothétie c est claire mais je ne vois pas pour la rotation comme je l indique dans la photo suivante

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 09 Déc 2018, 09:32
par Carpate » 09 Déc 2018, 09:32
Réponse à ta question
"comment on traduit ça dans C en utilisant les affixes de M, M',

Ben en utilisant la définition de l'affixe d'un point.
L'affixe d'un point
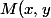)
dans un repère orthonormé
)
est le complexe
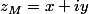
et l'on a

et
= (\vec{Ox},\vec{OM}))
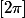
Je rebaptise

en C pour facilités LaTex.
Donc l'affixe du vecteur
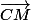
est


se traduit en

ou

 = \omega)
se traduit en
-arg(z_M-z_C)=\omega)
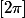
ou encore
=\omega)
On a donc

et
=\omega)
c'est donc que

et que
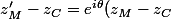)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités

