De retour avec l'algèbre : besoin d'explication

par **Elvis** » 12 Déc 2007, 21:17

Bonsoir,

Je remets une discussion en place, vue qu'elle ne passionne pas le foules. J'aurais simplement besoin d'une petite explication concernant l'exo suivant :

" Combien d'anneaux commutatifs (unitaires) y a-t-il, à isomorphisme près, de cardinal 0,...,6"

ThSQ m'a éclairé sur le sujet, mais mon problème est le suivant :
"si on considère un élément à 4 élements X = {0,x,y,z} avec 0 élement neutre pour l'addition. Il y a 4 choix pour 0 puis 3 choix pour l'élément neutre 1 de la multiplication. Donc je ne comprends pas trop comment tu trouves 2 solutions pour les groupes commutatifs ... Je sais pas si j'ai bien expliqué mon problème ..."

Merci d'avance

par **ThSQ** » 12 Déc 2007, 21:40

Je t'ai répondu (comme j'ai pu ...) sur l'autre thread.

Le plus surprenant c'est qu'il n'y a qu'un seul (sauf erreur bête de ma part) anneau à 6 éléments !!!

par **leon1789** » 12 Déc 2007, 22:02

ThSQ a écrit:Je t'ai répondu (comme j'ai pu ...) sur l'autre thread.

Le plus surprenant c'est qu'il n'y a qu'un seul (sauf erreur bête de ma part) anneau à 6 éléments !!!

il n'y a qu'un seul anneau commutatif à 6 éléments,
car il y en a aussi

mais non commutatif.

par **ThSQ** » 12 Déc 2007, 22:05

Oui bien sûr, on nous demandait les anneaux commutatifs.

Si tu pouvais répondre sur le fond du pb ça serait bien aussi .....

par **leon1789** » 12 Déc 2007, 22:45

Ha oui, j'avais mal lu et compris groupes commutatifs, mais on nous demandait les anneaux commutatifs...

par **Elvis** » 12 Déc 2007, 22:51

Ya pas de mal, et alors, une petite idée ?

par **yos** » 12 Déc 2007, 22:54

leon1789 a écrit:il n'y a qu'un seul anneau commutatif à 6 éléments,
car il y en a aussi mais non commutatif.

S_3 est pas un anneau.
On veut la commutativité pour la seconde loi. Celle de la première loi fait partie de la définition d'anneau.

par **leon1789** » 12 Déc 2007, 23:14

Effectivement, il n'y a qu'un seul anneau commutatif de cardinal 6, mais ce n'est pas exceptionnel (tout nombre sans facteur carré vérifie la même propriété) : une justification un peu (trop) technique peut être la suivante.

Soit I un idéal maximal d'un anneau A à 6 éléments : on a

où p est un diviseur premier de 6. Puis on démontre (théorème chinois) que A est isomorphe aux produit de quotients du type

où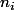

est inférieur à l'exposant de p dans l'écriture de n...

Ici, avec un cardinal égal à 6, on n'a pas le choix car

l'anneau est obligatoirement isomorphe à

par **leon1789** » 12 Déc 2007, 23:15

yos a écrit:S_3 est pas un anneau.
On veut la commutativité pour la seconde loi. Celle de la première loi fait partie de la définition d'anneau.

:we: oui, tu as raison, mais j'avais lu en diagonale et je me suis mis à confondre groupe et anneau... :help: je dois être fatigué :dodo:

par **ThSQ** » 13 Déc 2007, 20:29

leon1789 a écrit:Effectivement, il n'y a qu'un seul anneau commutatif de cardinal 6, mais ce n'est pas exceptionnel (tout nombre sans facteur carré vérifie la même propriété) : une justification un peu (trop) technique peut être la suivante.

Soit I un idéal maximal d'un anneau A à 6 éléments : on a où p est un diviseur premier de 6. Puis on démontre (théorème chinois) que A est isomorphe aux produit de quotients du type où est inférieur à l'exposant de p dans l'écriture de n...

Ici, avec un cardinal égal à 6, on n'a pas le choix car
l'anneau est obligatoirement isomorphe à

Très très intéressant merci Léon !

Ca prouve au passage que si |A|=p premier alors A est un corps ~= Z/pZ,+,. :doh:

De retour avec l'algèbre : besoin d'explication

De retour avec l'algèbre : besoin d'explication

Qui est en ligne