Résoudre inéquation

[Tvasse]

Bonjour.
Pour mon TD je dois trouver les extremums d'une fonction de 2 variables les qualifier et dire si ils sont globaux ou locaux.

La fonction est: H(x;y)= 4xy - x^4 - y^4

J'ai fais la plupart mais il me reste à déterminer le caractère global ou local des max en (-1;-1) et (1;1).

Je n'arrive pas a résoudre l'équation H(x;y) inférieur ou égal à H(-1;-1) = H(1;1)

Merci de m'aider

[Tiruxa]

Bonjour.
Pour mon TD je dois trouver les extremums d'une fonction de 2 variables les qualifier et dire si ils sont globaux ou locaux.

La fonction est: H(x;y)= 4xy - x^4 - y^4

J'ai fais la plupart mais il me reste à déterminer le caractère global ou local des max en (-1;-1) et (1;1).

Je n'arrive pas a résoudre l'équation H(x;y) inférieur ou égal à H(-1;-1) = H(1;1)

Merci de m'aider

En développant 2(x-y)² +(x²-1)² + (y²-1)² tu devrais pouvoir conclure car cette quantité est positive et ne s'annule que pour les couple (1,1) et (-1,-1)

[Ben314]

Salut,
Je pense que tu peut t'en sortir avec une bête étude de fonctions :
Pour fixé, la fonction a pour dérivée donc elle est croissante sur puis décroissante sur .
On en déduit que pour tout réel (et tout réel )
Ensuite, a pour dérivée 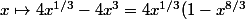dont on étudie le signe façilement...