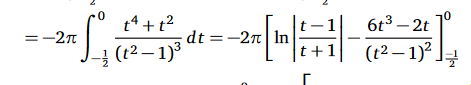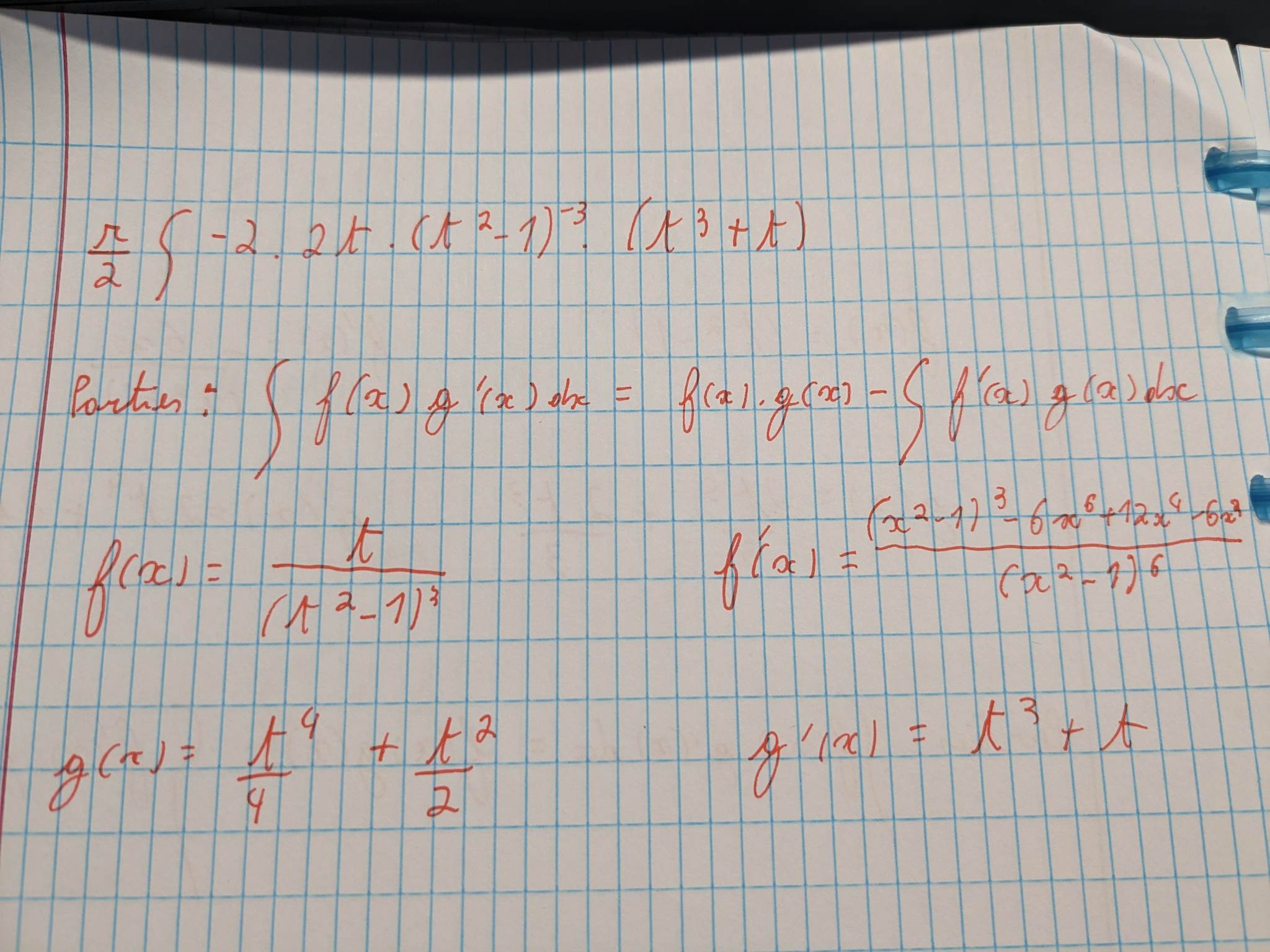Résolution d'intégrale

[ThéoBioIngé]

Bonjour à tous,

Voici une intégrale que je ne comprends pas comment résoudre. Il s'agit d'une résolution avec l'intégrale déjà simplifiée à coté mais je ne comprends pas comment celle si a été résolue car le détail n'est pas indiqué. Si quelqu'un pouvait m'expliquer cela me sauverait car j'aurai un test sur ce sujet dans quelques jours... Merci beaucoup!

[Ben314]

Salut,
Commence par une intégration par parties :


P.S. : Une intégrale, c'est un nombre et pas une équation donc ça ne se "résous" pas, ça se calcule.

[ThéoBioIngé]

Merci pour la réponse et la précision,

J'ai beau essayer les différentes possibilités, je ne vois pas quoi choisir comme f(x) et g(x) dans l'intégration par partie.

[Ben314]

Le but du jeu, c'est de diminuer le degrés du dénominateur et comme la dérivée de c'est où l'exposant du dénominateur est plus grand, ça signifie que pour diminuer le degré du dénominateur, il faut l'intégrer et pas le dériver.
Donc dans l'IPP, il faut qu'on ait c'est à dire

Sinon, tu peut aussi ne pas faire d'IPP et directement cherche la décomposition en élément simple de ta fonction, mais bon, vu que là, ça permet de diminuer le degré avec peu de calculs, moi j'aurais sans doute commencé par une IPP.

[catamat]

Bonjour

Il ya quand même un problème car la dérivée de la primitive proposée ne redonne pas la fonction de départ... il y a un coefficient 8.
Soit

et


on a

et

d'où

[koomath]

Donne la solution :