Résolution d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
berurier
- Messages: 5
- Enregistré le: 13 Juil 2009, 16:16
-
 par berurier » 13 Juil 2009, 17:08
par berurier » 13 Juil 2009, 17:08
bonjour tous le monde,
je doit résoudre ceci:
lim [r->0] ( int[0 pi] (1/(r.exp(2jO).exp(jr.exp(jO)(x-x0)))
- int[-a +a] (1/(r^2).exp(jr(x-x0))) )
ps: il y a pas un moyen de collé une expression maththype pk la :doh: ...
je pense que les deux integrale tende ver +infinie, et on obtien +infinie-infinie.
je voudrai donc résoudre les deux intégrale et fair la limite de l'expression obtenue.
si tout ce passe bien on devrais obtenir qq chose qui resemble a une constante pour 0
mais bon si ca ce passe mal c pas grave...
merci d'avance pour vos remarque.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 13 Juil 2009, 18:27
par sky-mars » 13 Juil 2009, 18:27
salut
pour facilité la lecture pour tout le monde
 e^{2j_{0}}}}{r e^{2j_{0}}}dr-\int_{-a}^{+a}\frac{e^{j r (x-x_{0})}}{r^2}dr))
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 13 Juil 2009, 18:37
par sky-mars » 13 Juil 2009, 18:37
Je pense que :
Pour la premiere intégrale tu fais une majoration et tu montres que c'est nul.
Pour la seconde tu la calcule ^^
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 13 Juil 2009, 18:49
par sky-mars » 13 Juil 2009, 18:49
 e^{2j_{0}}}}{r e^{2j_{0}}}dr)
sin(2j_{0})}}{r})
Pour
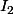
(= ton intégrale de -a à a etc..) fait une IPP et une majoration et sa devrait le faire
-
berurier
- Messages: 5
- Enregistré le: 13 Juil 2009, 16:16
-
 par berurier » 13 Juil 2009, 19:40
par berurier » 13 Juil 2009, 19:40
merci pour tes reponces,
j'ai deux trois question:
je comprent pas pk tu dit que exp(-r...)/r ->0 quand r->0: exp(-r)->1 et 1/r -> infinie, donc le produit tend ver l'infinie?
pour I2 j'avais deja test l'IPP, mais j'en etait resté la...
pour la majoration ca permet uniquement de montré que l'integral tend ver 0? non?
sinon il fau aussi faire une minoration??
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 14 Juil 2009, 06:32
par sky-mars » 14 Juil 2009, 06:32
OupS ^^' dans ma tête j'ai cru que r tendait vers l'infini et pas 0.
Je vais revoir ca

.
La majoration en valeur absolue, ui , est utilisé quand on veut montrer que quelque chose tend vers 0 et du coup tu n'as pas besoin de minoration.
Pour ton intégration par partie qui as tu intégré ? et qui as tu dérivé ?
En intégrant par partie je trouve
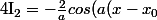) +<br />j(x-x_{0})\int_{-a}^{+a} \frac{e^{j r (x-x_{0}) }}{r }dr)
dommage que r ne tende pas vers

...
au fait a c'est quoi ?
Sinon
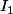
diverge quand r tend vers 0 et
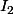
beh m'a fois je dirai oui si a ne tend pas vers

car

existe ...
-
berurier
- Messages: 5
- Enregistré le: 13 Juil 2009, 16:16
-
 par berurier » 14 Juil 2009, 11:06
par berurier » 14 Juil 2009, 11:06
heu oups j'ai fai une erreur, dans I2 le a est en fait r (le meme qui tend ver 0)
et du coup les deux integral diverge il me semble, ce qui donne +infinie-infini
ca vien de me fair pensé a un truc il serai pas plus simple de fair un developemen limité de cos et sin ??
sinon pour mon ipp je l'ai fai deux foix ce qui me donne int( ln(r) * exp(...) )
mais bon ca ma pas plus avancé qe ca ;)
en tout cas merci de t'interecé a mon problem
-
berurier
- Messages: 5
- Enregistré le: 13 Juil 2009, 16:16
-
 par berurier » 17 Juil 2009, 01:57
par berurier » 17 Juil 2009, 01:57
quelqu'un voi une solution a mom problem ?
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 17 Juil 2009, 06:39
par sky-mars » 17 Juil 2009, 06:39
salut,
essaie de faire un effort sur l'orthographe sinon les modérateurs vont te tomber dessus.
C'est juste un conseil que je te donne.......
Pour ton problème, où as tu eu ces équations?
-
berurier
- Messages: 5
- Enregistré le: 13 Juil 2009, 16:16
-
 par berurier » 17 Juil 2009, 11:17
par berurier » 17 Juil 2009, 11:17
désolé pour mon orthographe mais je ne suis vraimen pas trés fort dans ce domaine...
ces equations viennent d'une transformé de fourier inverse d'une impedance Z de la forme 1/k^2*coth(k^2).
la transformé de fourier inverse explique l'integrale de -l'infinie a +l'infinie et l'exponentiel de -jk(x-x0) (x0 etant un décalage).
pour résoudre cette equation je suis passé par le theoréme des résidues sur le demie cercle supérieur.
la racine etant en 0, j'ai prie un demie cercle qui contourne le 0 avec un rayon qui tend ver 0 pour ne pas avoir a calculé les résidues, ce qui explique le r qui tend ver 0 et l'integral de 0 a pi (demie cercle)
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 17 Juil 2009, 15:26
par sky-mars » 17 Juil 2009, 15:26
Déjà tu me parle de 0 alors que tu es sensé me parler de pôle ...
car normalement
 dz = 2i\pi \sum_{k} Res(f,z_{k}))
Au départ tu avais une impédance :
}{k^2})
Est-ce ça ou j'ai mal écrit la formule que tu voulais me dire ?
L'intégrale de -

à

c'est celle qui a pour borne -a et +a c'est ca ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
