Réduction d'une matrice

[morlock84]

Bonsoir, j'aurais besoin d'un peu d'aide sur ce résultat. On prend telle que rg(A) = 2n et A^3 = 0. Il faut montrer que A est semblable à :




A est équivalente à la matrice ci-dessus, et la nilpotence implique que A est semblable à une matrice triangulaire supérieure stricte, mais là je suis en panne d'angle d'attaque... merci d'avance !

[zygomatique]

salut

soit f l'endomorphisme associé à A ....

puisque on est en dimension finie le théorème du rang nous permet de dire que Dim(Ker f) = n

donc il existe n vecteurs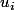 et 2n vecteurs 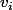tel que leur union forment une base et dans laquelle la matrice de A est formée de n colonnes de 0

de plus évidemment pour tout i et forment une base de Im f ...


or car la seule valeur propre de f est 0

pour tout vecteur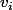 la famille est libre

donc parmi les 2n vecteurs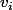 on peut en choisir n tels que soit une base de Im f

montre que la famille conduit à la première marice et que la famille conduit à la deuxième matrice


on va avoir les deux cas ::



en gros .... :lol3:

[morlock84]

Merci de votre réponse, mais il n'y a pas un problème ?

[zygomatique]

ha oui damned ...


soit f l'endomorphisme associé à A ....

puisque on est en dimension finie le théorème du rang nous permet de dire que Dim(Ker f) = n

donc il existe n vecteurs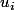 et 2n vecteurs 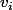tel que leur union forment une base et dans laquelle la matrice de A est formée de n colonnes de 0

de plus évidemment pour tout i et forment une base de Im f ...

donc parmi les 2n vecteurs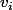 on peut en choisir n tels que soit une base de Im f

montre que la famille conduit à la première marice et que la famille conduit à la deuxième matrice


on va avoir les deux cas ::



en gros .... :lol3:


d'ailleurs je dirais même que pour tout i 1=< i =< n


pour dégrossir il me semble ....

[paquito]

Si tu prends;tu as un déterminant de rang 2 non nul; donc rang(A)=2 et ,mais qui est de rang 1: il existe donc un vecteur non nul tel que soit non nul;en posant et , on vérifie facilement que est une base de E dans laquelle la matrice f s'écrit:
.
Dans le cas général, Il est clair que, l'idée est de montrer que , donc que rang(f²)=n;
supposons que rang(f²)>n;dans ce cas on ne pourrait pas avoir Im f²\subset Ker f et donc pas non plus ; on ne peut pas non plus avoir rang (f²)<n car dim kerf² 2n (on a 2n quand ker f \subset Imf) donc finalement rang (f²)=n.
Choisissons une base de Im f²;alors dans la base
,la matrice de f s'écrit comme désirée.