Recherche d'un supplémentaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 09 Juil 2007, 20:37
par fenecman » 09 Juil 2007, 20:37
Bonsoir,
je ne vois pas par où commencer cet exercice. Si quelqu'un veut me débloquer il est le bienvenu :we: .
Voilà l'exercice:
Soit E l'ensemble des fonctions continues de [0,1] à valeurs réelles et soit
=0\})
Et on demande de trouver un supplémentaire de F dans E.
Merci d'avance
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 09 Juil 2007, 21:15
par emdro » 09 Juil 2007, 21:15
Bonsoir,
si tu appelles

une fonction continue non nulle en
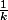
, mais nulle en tous les autres
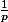
pour p entre 1 et 10.
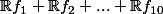
doit être un supplémentaire de F.
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:16
par Ledescat » 09 Juil 2007, 21:16
emdro a écrit:Bonsoir,
si tu appelles

une fonction continue non nulle en
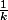
, mais nulle en tous les autres
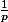
pour p entre 1 et 10.
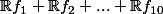
doit être un supplémentaire de F.
La fonction nulle doit appartenir au supplémentaire pour qu'il soit un sev (à moins qu'on ne parle pas d'espaces vectoriels , dans ce cas je me tais :we: ).
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 09 Juil 2007, 21:21
par emdro » 09 Juil 2007, 21:21
Merci Rain' de m'éviter de poster la même réponse!
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:22
par Ledescat » 09 Juil 2007, 21:22
emdro a écrit:Merci Rain' de m'éviter de poster la même réponse!
Mais je sais pas ce que j'ai avec les Vect en ce moment ! Il faut vraiment que je me repose (cf hier mon ev des AB-BA :we: ).
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 09 Juil 2007, 22:12
par fenecman » 09 Juil 2007, 22:12
Rain' a écrit:Soit
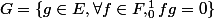
En bref, G est le supplémentaire orthogonal de F dans E pour le produit scalaire
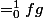
Merci de l'aide, cependant il y a quelque chose qui me chagrine : Si on prend G=l'espace fourni par emdro , comment être sûr que l'intégrale de g*f sur 0,1 va être nulle pour tout f appartenant à F puisque comme g est continue , g est nulle sur un voisinage de 1/k mais il faut que f soit nulle au dehors de ce voisinage, donc si f est non nulle sur un voisinage de 1/k qui dépasse celui de g alors l'intégrale ne sera pas nulle.
A moins que l'espace fourni par Emdro ne soit pas un supplémentaire orthogonal?
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 10 Juil 2007, 04:24
par B_J » 10 Juil 2007, 04:24
fenecman a écrit:Bonsoir,
Soit E l'ensemble des fonctions continues de [0,1] à valeurs réelles et soit
=0\})
Et on demande de trouver
un supplémentaire de F dans E.
le supplementaire d'un sev n'est pas unique
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 10 Juil 2007, 10:00
par fenecman » 10 Juil 2007, 10:00
D'accord!
Cependant je n'arrive pas à montrer rigoureusement que le sev fourni par emdro est un supplémentaire :mur: .Je suis d'accord que l'intersection entre F et le supplémentaire est réduite à {0}, mais pour montrer E=F+S je bloque...
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 10 Juil 2007, 10:14
par emdro » 10 Juil 2007, 10:14
Bonjour,
prends une fonction de E. On va la décomposer en la somme d'une fonction de F et d'une de mon sev S.
Ecrivons
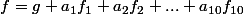
où g est dans F.
Les fonctions doivent coïncider sur les
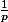
. Mais toutes les fonctions de droite sont nulles en
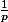
sauf
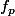
.
Donc nécéssairement:
=a_pf_p(\frac{1}{p}))
Cela te fixe ton
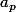
(de manière unique).
Et c'est gagné, car la fonction g définie par
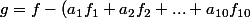)
sera bien dans F, par construction.
Edit: grillé par Rain'!
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 10 Juil 2007, 10:18
par emdro » 10 Juil 2007, 10:18
Rain' a écrit: les fonctions f_k d'emdro valent 0 en 1/p pour p dans [|1,10|] entier différent de k, et 1 en 1/k.
Je connaissais les polynômes de Lagrange, la fonction de Riemann... Les fonctions d'emdro, cela me flatte terriblement... :doh:
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 10 Juil 2007, 10:57
par fenecman » 10 Juil 2007, 10:57
Merci bien,
Ces raisonnements par Analyse/Synthèse me jouent toujours des tours!!!
Je ferais attention maintenant :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
