Recherche d'un équivalent

par **fenecman** » 22 Déc 2007, 15:55

Bonjour, pouvez vous m'aider à trouver un équivalent de (Un) en +

si :

Merci
(J'ai déjà réussi à montrer que

diverge, je pensais ensuite utiliser le théorème de sommation des relations de comparaisons mais je bloque..)

Oups... j'ai posté deux fois . Désolé :briques:

par **ThSQ** » 22 Déc 2007, 16:22

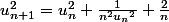
Ca prouve que

et donc diverge et que

existe
Après tu sommes tout et je te laisse finir :zen:

par **fenecman** » 22 Déc 2007, 17:12

En faisant passer

à gauche, je somme tout , j'obtiens alors que

C'est ça?

par **yos** » 22 Déc 2007, 18:52

ThSQ a écrit: et donc diverge

Bonsoir.
J'ai pas tout compris.
Partons de

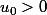
. La suite

est croissante donc si elle converge, sa limite est un réel

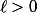
. C'est impossible comme on le voit en faisant tendre n vers

dans la relation de récurrence. Donc

tend vers

.
Après on peut enchaîner sur ce qu'a fait Teachescu.

par **ThSQ** » 22 Déc 2007, 19:00

yos a écrit:Bonsoir.
J'ai pas tout compris.

C'était des indications pas une solution "finie".

de

il est pas trop dur de déduire que

et donc une divergence immédiate :happy2:

par **leon1789** » 22 Déc 2007, 19:00

yos a écrit:Bonsoir.
J'ai pas tout compris.
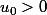
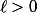
Partons de . La suite est croissante donc si elle converge, sa limite est un réel . C'est impossible comme on le voit en faisant tendre n vers dans la relation de récurrence. Donc tend vers .
Après on peut enchaîner sur ce qu'a fait Teachescu.

Effectivement, la monotonie de la suite dépend du signe de son premier terme.
En revanche, le passage à la limite de la relation de récurrence donne

...

par **ThSQ** » 22 Déc 2007, 19:04

fenecman a écrit:En faisant passer à gauche, je somme tout , j'obtiens alors que
C'est ça?

:++:

On a même un développement asymptotique en fêtes (de Noël)

par **yos** » 22 Déc 2007, 19:07

leon1789 a écrit:En revanche, le passage à la limite de la relation de récurrence donne ...

Ah oui ça fait

: vachement intéressant. Donc il vaut mieux sommer les

pour avoir la divergence.

par **fenecman** » 22 Déc 2007, 19:20

Au fait on écrit comment le symbole "équivalent" en TEX ?

par **ThSQ** » 22 Déc 2007, 19:30

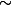
= \sim

par **fenecman** » 22 Déc 2007, 20:08

Merci !! sim comme similar je suppose!

par **ThSQ** » 22 Déc 2007, 21:59

fenecman a écrit:Merci !! sim comme similar je suppose!

Peut-être. C'est pas toujours hyper clair de savoir d'où vient le nom des commandes Latex :hum:

Recherche d'un équivalent

Recherche d'un équivalent

Qui est en ligne