Recherche equation avec asymptote oblique

[Serge Remicoure]

Bonjour,

N'ayant plus fait de math depuis un sacré bout de temps, je cherche une bonne ame pouvant m'aider à formuler mathématiquement une fonction qui je pense est assez simple.

Je cherche une fonction qui augmente de la même manière qu'une fonction f(x) = ;)(x) mais avec une asymptote y = 100 !
Cette fonction serait définie de 0 à l'infi.

Merci d'avance à celui ou celle qui pourra m'aider.

Serge

[DamX]

Bonsoir,
est-ce que

Conviendrait ? Avec le niveau de l'asymptote.

Proche de 0 cette fonction se comporte comme racine(x) comme demandé et converge asymptotiquement vers y=a.

Damien

[Robic]

Tiens, il y avait eu une question semblable il y a une ou deux semaines, mais avec une asymptote à 64. Si la fonction doit partir de 0, croître puis tendre vers 100, on peut faire par exemple :
f(x) = 100 x / (x + 100)
g(x) = 100 (1 - exp(-x))
h(x) = (200 / Pi) arctan( x )

(Mais ces fonctions ne sont pas équivalentes à la racine carrée au voisinage de 0.)

[Serge Remicoure]

Genial, merci à tous les 2 pour vos réponses Damx et Robic. J'ai testé vos différentes équations et c'est exactement ce que je recherchais.

Maintenant si je peux me permettre, j'aimerais complexifier un petit peu le probleme..

Comment pourrait-on faire en sorte que, de 0 à environ 95, la fonction se rapproche le plus possible de la droite y=x tout en restant plafonnée à y=100 lorsque x est supérieur à 95?

[Robic]

Dans ce cas, une méthode peut être de définir la fonction par deux formules selon l'intervalle :
- Pour x dans [0 ; 95] : f(x) = x.
- Pour x > 95 : f(x) = 100 - 25/(x-90).

En procédant ainsi, on a construit une fonction continue et dérivable en 95 (mais pas deux fois dérivable).

[Serge Remicoure]

Bien vu Robic ! Ca me semble très bien.

Pour la petite info, je gère un projet d'application smartphone dans laquelle va être intégré, entre autre, une barre de progression destinée à estimer la la qualité d'une entreprise. Plutôt que de faire une moyenne de plusieurs évaluations, la façon dont je l'envisage, c'est que les utilisateurs pourront donner 1, 2 ou 3 points à l'entrepise ou au contraire en retirer 1,2 ou 3. Le score le plus bas sera 0, et comme aucune entreprise n'est parfaite, je souhaite qu'elle n'atteigne jamais le score de 100% car il y'a toujours quelque chose à améliorer...

Si vous avez des remarques ou des suggestions à me faire, elles sont les bienvenues !

Encore merci pour votre aide,

Serge

[deltab]

Bonjour.

Je cherche une fonction qui augmente de la même manière qu'une fonction f(x) = (x) mais avec une asymptote y = 100 !
Cette fonction serait définie de 0 à l'infi.

Qu'entends tu par "de la même manière qu'une"
Les solutions proposées sont bornées sur un intervalle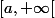 alors que la fonction est non bornée, admet une direction asymptotique mais pas d'asymptote.

[Robic]

Je pense que la question a été bien comprise. Serge voulait dire une fonction qui croît de moins en moins vite, comme la racine carrée, avec en plus une asymptote. De toute façon ses deux derniers messages sont clairs et précis.