Rapidité de convergence d'une suite

[totolivier]

bonjour

je me demandais comment se définissait la "rapidité" de convergence d'une suite.

intuitivement, ca doit forcément faire intervenir (Un-l), avec l sa limite, mais suivant quelle critère?

merci

[MacManus]

soit (n 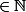) une suite et l sa limite.
la vitesse de convergence de la suite u peut être définie par le rapport suivant : ou p est un entier strictement positif. Plus p est grand, meilleur est la convergence.
Par exemple, pour p = 1, on parle de convergence linéaire, pour p = 2, on parle de convergence quadratique, etc...(on peut utiliser cette définition dans un développement de Taylor, pour définir la "rapadité" d'une méthode de convergence : méthode du point fixe - méthode de Newton - méthode de la corde ...)

Sauf erreur de ma part

[totolivier]

bjr

je n'ai pas tres bien compris...Si un=0, le rapport n'est plus défini. Imaginons que un non nul, à quoi correspond ce rapport sinon à une valeur? et le coefficient p à quoi il correspond puisqu'on aura tjs une valeur défini pour chaque n

[neuneu]

Bonjour on caractérise la vitesse de convergence d'une suite en étudiant la limite du rapport .
Si on appelle cette limite ( en supposant qu'elle existe) elle est toujours comprise entre 0 et 1.
On dit que converge lentement verssi =1
converge géométriquement vers si 0<<1
converge rapidemment vers si =0