Rapidité de convergence

[AceVentura]

Bonjour à tous.

On considère une suite de la forme avec , et une suite de limite nulle.
(i) La suite converge lentement vers .
(ii) La suite converge vers plus vite que la suite .



Alors pour le (i), j'aimerai écrire . Mais le dernier terme de la suite est de la forme 0/0. J'ai donc écrit car est une suite de limite nulle. On conclut avec le théorème d'encadrement.
Et ici j'ai un doute. Pour pouvoir parler de coefficient de convergence, il faut que pour tout n ?
Ensuite, il s'agit de regarder la limite du rapport et qui converge vers 1 : on a donc la convergence est bien lente.


Ensuite pour le (ii), on regarde le coefficient de convergence de la suite et on le compare à celui de la suite . La suite a pour limite mais je n'en suis pas certain. Si , est-ce que ?
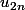
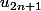
(C'est d'ailleurs l'occasion pour moi de vous poser une autre question : si et converge vers la même limite, a-t-on que converge et vers cette limite commune ?)
On poursuit en regardant la limite du rapport : mais je trouve 1. Je ne peut donc pas conclure

[alavacommejetepousse]

bonsoir

ce n est pas indéterminé c 'est "0x0" et non " 0/0"

[AceVentura]

Oui, c'est vrai !
Pour pouvoir parler du coefficient de convergence, faut-il donc bien que ?

[Ben314]

Non, ce n'est pas indispensable, comme tout ce qui concerne les limites, on peut se contenter d'avoir pour tout n à partir d'un certain rang.
Par exemple pour ta suite on a uniquement lorsque ce qui est forcément faux à partir d'un certain rang vu que Vn tend vers 0 et que b est non nul.

[AceVentura]

Ok. En fait, j'ai du mal à comprendre le cadre d'une telle leçon. Je te l'avais demandé déjà dans un autre fil. Il est écrit que est une suite réelle ayant une limite finie et on suppose que non stationnaire.
Alors je sais pas trouver un critère pour décider s'il existe ou non un coefficient de convergence pour une suite donnée.

[Ben314]

Le "coeff. de convergence" est défini comme la limite d'un quotient.
Pour qu'un quotient existe, il faut que son dénomiateur soit non nul, mais pour pouvoir étudier la limite d'une suite, il suffit que les termes de la suite soit définis "à partir d'un certain rang".
Si on te demande la limite de la suite Un=1/(n-500) est ce que ça te dérange franchement que, pour n=500, Un n'existe pas ?
En général, dans le "cours", pour simplifier, on écrit les suites: , alors que dans les exercices, elle peuvent trés bien commencer à n=1 ou n=501 ou..., ça ne change rien en ce qui concerne les limites.

[AceVentura]

Ok, ok
J'ai une proposition dans mon cours qui me dit que si alors la convergence est lente vers l.
Ici, n'a-t-on pas que, pour , ?

Par contre je n'arrive pas à prouver que la suite converge plus rapidement que la suite vers a.

[Ben314]

J'avais pas regardé tout ton post de départ...

La suite a pour limite mais je n'en suis pas certain. <- c'est bien ça, d'ailleurs l'énoncé te le dit...
Si , est-ce que ? Oui : si Un admet une limite alors toute suite extraite de Un (i.e. en prenant un terme de temps en temps) converge elle aussi vers la même limite.
(C'est d'ailleurs l'occasion pour moi de vous poser une autre question : si et converge vers la même limite, a-t-on que converge et vers cette limite commune ? Oui : il faut utiliser la définition des limites pour le démontrer... )
On poursuit en regardant la limite du rapport <- Ici, tu sait que l=a : mais je trouve 1 tu as du te tromper, recommence les calculs....

Tu devrais aussi appeller ta troisième suite Wn et pas Vn, vu qu'il y en a déjà une dans l'énoncé qui s'appele Vn...

[Ben314]

Non, j'ai dit une connerie, on ne peut pas déterminer la limite du rapport : cela dépend de la suite de départ.

Ici, "montrer que tend vers plus vite que " signifie qu'il faut montrer que le rapport tend vers 0.

[AceVentura]

Puis quand je passe à la limite, je trouve bien 1, non ?
:hein:

EDIT : en effet, on obtient une FI de la forme 0/0

[Ben314]

Non, pour le moment, c'est une trés belle forme indéterminée de la forme 0/0 vu que tout les U? tendent vers a.
Il faut que tu remplaces les U? par leur définition respectives et là, tu va de nouveau te retrouver... avec une forme indéterminée contenant des V? que tu ne connait pas...

[AceVentura]

et le passage à la limite donne toujours une FI non ?

[AceVentura]

Peut-être était-il préférable d'écrire : on suppose que la suite converge vers de façon lente ?

[Ben314]

et le passage à la limite donne toujours une FI non ?

Pour le moment oui, mais il faudrait que tu remplace les U? par leur définition pour n'avoir que des V? dans ta formule.
Cela te permet de "lever" l'indétermination et de trouver que cette limite vaut 0.

[AceVentura]

Merci bien Ben. Cela marche très bien :)

[AceVentura]

Je me demande ou a-t-on utilisé le fait que b était non nul :hein:
ne pose donc aucun problème si a=0
car sinon on va avoir un problème au niveau de la limite de .
mais pour le ?

[AceVentura]

J'ai une autre question.
est une fonction continue et est la subdivision définie par . On définie alors la suite avec . Il faut expliquer pourquoi la suite n'est pas accélérable.

Une idée ?

[Ben314]

Je me demande ou a-t-on utilisé le fait que b était non nul :hein:
ne pose donc aucun problème si a=0
car sinon on va avoir un problème au niveau de la limite de .
mais pour le ?

Que a soit nul, positif ou négatif, on s'en fout complètement vu que, dans tout les calculs c'est (Un-a) qui apparait.
Par contre, si b est nul, on ne peut surement pas conclure car, vu que l'on ne connait pas Vn, on n'a quasi aucun contrôle sur la vitesse de convergence de Un.
Déjà, si b est nul, tu ne peut pas montrer que Un est distinct de a pour n assez grand, ni montrer que la vitesse de convergence de Un vers a est "lente" et je suis persuadé que tu ne peut pas montrer que Wn tend "plus vite" vers a que Un : regarde bien tes calculs et tu verra que "b non nul" sert tout le temps (en particulier, il doit y avoir de nombreux dénominateurs qui tendent vers b...)

[Ben314]

J'ai une autre question.
est une fonction continue et est la subdivision définie par . On définie alors la suite avec . Il faut expliquer pourquoi la suite n'est pas accélérable.

Une idée ?

Trés honètement, je n'ais aucune idée du fait qu'il me faudrait une définition "carrée carrée" de ce que l'on appelle "accelerer" une suite.
Par exemple, il me semble qu'en prenant Q(n)=P(f(n)) où f:N->N est une fonction qui tend "trés trés vite" vers l'infini, la suite Q tendra plus vite que P vers la même limite...

Où alors, cela se réfère juste à la partie précédente, c'est à dire que l'on doit montrer que P(n) n'est pas de la forme ...

[AceVentura]

Salut Ben.
On se donne une suite de nombres réels ayant pour limite .
est un procédé d'accélération de convergence si :
1)
2) converge vers plus rapidement que

C'est la définition que j'ai.
Il faut, je pense, démontrer qu'il n'existe pas de tel procédé.