Racines quatrième d'un nombre complexe avec argument = arc-t
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 02 Nov 2021, 19:28
Bonsoir
Je cherche la racine quatrième de
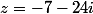
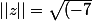^2+(-24)^2}=\sqrt{49+576}=\sqrt{625}=25)
= \left\lbrace\begin{matrix}<br />cos \: \theta = \frac{-7}{25} \\ <br /> isin \:\theta = \frac{-24}{25}<br />\end{matrix}\right. \Longrightarrow -\pi +artan \bigl(\begin{smallmatrix}<br />\frac{24}{7}<br />\end{smallmatrix}\bigr))
On a
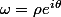
tel que
})
<br />\end{matrix}\right. \Longleftrightarrow \left\lbrace\begin{matrix}<br /> \rho = \sqrt[4]{25}\\ <br /> \theta =-\frac{\pi}{4} + \textcolor{red}{\frac{artan \bigl(\begin{smallmatrix}<br />\frac{24}{7}<br />\end{smallmatrix}\bigr)}{4}} +\frac{2k\pi}{4}<br />\end{matrix}\right.)
C'est la première fois que j'utilise arc-tangente avec les nombres complexes, je ne le manipule pas souvent.
Je suis un peu perdu au niveau de la zone rouge.
Est-ce que je peux diviser un arc-tangente par un nombre comme ci-dessus ?
A bientôt
-
azf
par azf » 02 Nov 2021, 20:24
bonjour
ok pour l'argument principal dans
mais moi je préfère utiliser arccos pour trouver l'argument
Lorsque
\geq 0)
alors
}{\left|\left|z\z\right|\right|}\right))
sinon
}{\left|\left|z\z\right|\right|}\right))
vous devez donc trouver les
quatre racines du polynôme
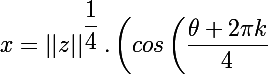+i.sin\left(\dfrac {\theta +2\pi k}{4}\right) \right))
avec
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 02 Nov 2021, 20:52
Bonjour,
on peut aussi résoudre l'exercice en utilisant uniquement des factorisations
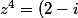^4)
^4=[z^2+(2-i)^2][z^2-(2-i)^2]=[z^2-i^2(2-i)^2][z^2-(2-i)^2])
^2][z^2-(2-i)^2]=[z+i(2-i)][z-i(2-i)][z+(2-i)][z-(2-i)])
d'où les 4 racines
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 02 Nov 2021, 21:15
Bonsoir
Merci pour vos observations !
Mais il faut que j'utilise l’exponentielle.
Je reviens à ma question peut on diviser l'arc-tangente ?
A bientôt
-
azf
par azf » 02 Nov 2021, 21:23
la seule chose qu'il est interdit de faire c'est de diviser un angle par zéro
votre arc tan est un angle et ici vous divisez votre angle par 4
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 02 Nov 2021, 21:29
Donc j'obtiendrai
)
A bientôt
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
