Question sur un encadrement
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
soleil15
- Messages: 3
- Enregistré le: 05 Avr 2010, 21:18
-
 par soleil15 » 05 Avr 2010, 21:20
par soleil15 » 05 Avr 2010, 21:20
bonsoir
sachant que D est une constante et sachant que
|xn+1-a|je dois demontrer que a appartient à l'intervale[xn,xn+1]
comment faire?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 05 Avr 2010, 22:08
par Finrod » 05 Avr 2010, 22:08
Le fait que a soit entre

et

est équivalent au fait que

est alternée, i.e change de signe à chaque étape.
Donc, il doit surement y avoir d'autres hypothèses, car celle que tu donnes ne donne aucune conditon sur le signe.
-
soleil15
- Messages: 3
- Enregistré le: 05 Avr 2010, 21:18
-
 par soleil15 » 06 Avr 2010, 17:05
par soleil15 » 06 Avr 2010, 17:05
merci pour votre réponse déja
en fait c'est une question dans un problème
en dois résoudre f(x)=x²-a=0
on a xn+1=1-ln[1+exp xn]converge vers racine de a.
je sois montrer que la solution exacte x* de l'équation est comprise entre xn et xn+1.
et l'inégalité que j'ai donné auparaant est donnée au cours et j'ai cru que je pourrais résoudre avec laquelle.
voila alors qu'est ce que je peux faire??
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 06 Avr 2010, 17:11
par Finrod » 06 Avr 2010, 17:11
Il doit y avoir une erreur dans ta relation de récurrence, elle devait dépendre de f, pour que le limite dépende de a.
Edit : il faudrait
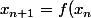+x_{n})
... (par ex)
-
soleil15
- Messages: 3
- Enregistré le: 05 Avr 2010, 21:18
-
 par soleil15 » 06 Avr 2010, 18:24
par soleil15 » 06 Avr 2010, 18:24
désolé
en fait on doit chercher une solution de l'équation ln(1+exp x ) = 1-x en considérant l'itération x_n+1 = 1-ln(1+exp x_n)
j'ai montré que cette itération converge vers un point x* mais je dois prouvé que x* est compris entre x_n rt x_n+1
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités