Question d'inégalité

[beranger21]

Bonjour à tous,
j'ai une question qui m'est posée, je me suis déjà penchée dessus,
mais je n'arrive pas à avancer, pouvez m'aider svp ?

Montrer que pour tout n>= 2:

1/k<=ln(k)-ln(k-1)

J'ai remarqué que ln(k)-ln(k-1) était la primitive de 1/k entre les bornes k-1 et k, mais je n'arrive pas à aller plus loin.

Merci d'avance

[Sa Majesté]

Salut

Tu as déjà une bonne piste.
La fonction 1/x étant décroissante sur [k-1,k], l'aire sous la courbe (qui vaut ) est supérieure à l'aire du rectangle de largeur k-(k-1) = 1 et de longueur 1/k.

[beranger21]

Salut,
déjà merci d'avoir répondu rapidement !
Oui mais il faut que je le démontre que l'aire de "lnk - ln(k-1)" est supérieure au rectangle... je pense à un encadrement de cette aire justement , mais je ne vois pas comment ... :mur: ^^

[Ben314]

Ben...
Sa majesté vient très exactement de te le dire...
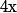Vu que est décroissante sur , c'est que, pour tout dans cet intervalle on a donc l'aire sous la courbe de (sur cet intervalle) est au moins égale à celle du rectangle de hauteur et au plus égale à celle du rectangle de hauteur .
Comme la largeur des deux rectangles est , ça te donne , c'est à dire