0 puissance 0

[melreg]

Bonjour,

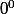
Peut-on calculer ? Ou est-ce que ça vaut 1 par définition, est-ce que c'est indéterminé?
La raison de ce post est que dans un de mes cours, il y a .

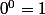
Merci

[MathMoiCa]

'lut,

Ce n'est pas pour faire de la pub, mais je connais cette discussion sur un autre forum qui est pas mal : http://forums.futura-sciences.com/thread166012.html


M.

[jimbo]

on ne peut pas la calculer c'est du n'importe quoi car ça n'a pas de sens!
la valeur de 0 puissance 0 est indéterminée!

[JJa]

Si tu veux en savoir plus sur les tenants et aboutissants du bizarre 0^0 , le dit "Monstre du Power Less" , un beau serpent de mer :
L'article : "Zéro puissance zéro", publié dans le magazine QUADRATURE, n°66, octobre 2007, pp.34-36.

[yos]

on ne peut pas la calculer

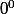
Mais on peut lui donner une valeur (convention). Comme lorsqu'on pose 0!=1 : c'est très pratique pour élargir le domaine de validité des formules. Pour , je peux affirmer que la valeur 1 est la plus pratique.

[nuage]

Salut,

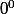
Mais on peut lui donner une valeur (convention). Comme lorsqu'on pose 0!=1 : c'est très pratique pour élargir le domaine de validité des formules. Pour , je peux affirmer que la valeur 1 est la plus pratique.

0!=1 relève de la continuité de la fonction
On ne peut pas en dire autant de .
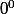
Même si, en probabilité ou pour les polynômes, c'est une convention utile et justifiable, il reste trop de problèmes en analyse.
:marteau:

[prody-G]

Mais on ne pourrait pas la considérer comme étant la limite de quand x tend vers ?

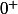
[ffpower]

ben pk x^x et pas 0^x par ex..

[yos]

0!=1 relève de la continuité de la fonction
On ne peut pas en dire autant de .
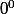
Même si, en probabilité ou pour les polynômes, c'est une convention utile et justifiable, il reste trop de problèmes en analyse.

Et pourquoi la fonction gamma plutôt que n'importe quelle fonction f prenant en les entiers n la valeur n! (ce que d'ailleurs ne vérifie même pas la fonction gamma)???
Quant aux "problèmes" dont tu parles, je ne vois pas trop lesquels.

[ffpower]

Je crois que la fonction gamma est la seule fonction interpolant n! et ayant une certaine régularité(mais ché plus trop laquelle:p-e holomorphe+une croissance contolee)

[prody-G]

ben pk x^x et pas 0^x par ex..

parce que par définition ça ferait ...et c'est pas très joli comme truc...

[JJa]

Ce 0^0, c'est vraiment le serpent de mer que l'on voit réapparaître dans les forums de maths.
Voici une phrase tirée de la conclusion de l'article que j'ai cité dans mon post précédent :
"Chacun aura compris que, si le domaine des mathématiques dans lequel on travaille n’est pas précisé, 0^0 est indéterminé. Il n’en va pas de même si l’on se place dans un contexte bien délimité, dans lequel une définition précise et spécifique à ce domaine a été donnée au formalisme 0^0."
Bien sûr, cette phrase n'est qu'une partie de la conclusion, puisque l'article passe en revue les domaines des mathématiques où l'on rencontre 0^0, avec des significations spécifiques à chaque domaine.
Ainsi, dire que 0^0 est indéterminé quel que soit le contexte est une prise de position un peu trop abrupte !

[raito123]

à droite de 0 on peut trouver que 0^0=1 mais à gauche je n'en suis pas si sûr !!!

[nuage]

Salut,

Et pourquoi la fonction gamma plutôt que n'importe quelle fonction f prenant en les entiers n la valeur n! (ce que d'ailleurs ne vérifie même pas la fonction gamma)???
Quant aux "problèmes" dont tu parles, je ne vois pas trop lesquels.

par exemple.

[yos]

par exemple.

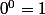
Avec la convention , ta fonction est pas continue. Est-ce bien grave? Il faudrait s'entendre sur ce que tu appelles "problème".

[nuage]

Salut yos
ce que j'appelle problème est le résultat suivant :
Si et alors peut prendre n'importe quelle valeur dans

[yos]

ce que j'appelle problème est le résultat suivant :
Si et alors peut prendre n'importe quelle valeur dans

Salut nuage.
Valeur positive quand même...
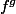
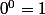
Si la limite est finie, tu l'appelleras la valeur de en 0. Ca ne me parait pas nuire à la convention . L'erreur serait d'inventer un théorème de plus sur les limites. Je pense pas qu'on puisse comparer ce cas à 0/0 pour lequel une convention genre 0/0=1 n'apporterait rien aux formules connues. Quoiqu'il en soit, quand un truc est pas défini, on a le droit de le définir : si possible de manière utile.

[nuage]

Salut yos,
pour la valeur positive je suis d'accord et j'ai rectifié.
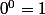
Je suis d'accord sur l'utilité de poser dans certains cas, et je le fait souvent, mais ces cas ne sont pas généraux.
Ce qui, à mon avis, explique l'absence de définition de .
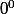
La valeur 1 pose trop de problème, même si elle est souvent pratique.