Bonjour,
Je bloque sur l'exercice suivant :
Je bloque sur comment effectuer la partie hérédité pour la récurrence, pour le 1/ j'ai trouvé que f(n) (x) = n f(x)
ce qui marche pour n=0 mais je ne sais pas comment il faut faire pour l'hérédité sachant que je veux montrer que f(n+1) (x) = (n+1) f(x)
Merci d'avance
Puissance fonctionnelle / recurrence
13 messages
- Page 1 sur 1
Re: Puissance fonctionnelle / recurrence
Alors j'ai encore plus besoin d'aide que je pensais.. Je n'ai honnêtement aucune idée même en ayant calculé avec les premiers n
Re: Puissance fonctionnelle / recurrence
Normalement j'ai trouvé la bonne propriété : f(n) (x) = f(x) x 2^(n-1)
Mais je ne sais pas le démontrer quand même
Mais je ne sais pas le démontrer quand même
Re: Puissance fonctionnelle / recurrence
Salut,
Y'a un truc que je comprend pas trop : pourquoi exprime tu}(x)) en fonction de f(x) et pas plus bêtement uniquement en fonction de x.
en fonction de f(x) et pas plus bêtement uniquement en fonction de x.
Par exemple, pour n=1, tu pense que c'est plus utile d'écrire comme tu le fait que f(x)=f(x) plutôt que d'écrire simplement f(x)=2x ?
Y'a un truc que je comprend pas trop : pourquoi exprime tu
Par exemple, pour n=1, tu pense que c'est plus utile d'écrire comme tu le fait que f(x)=f(x) plutôt que d'écrire simplement f(x)=2x ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Puissance fonctionnelle / recurrence
Fais la récurrence. Elle ne présente absolument aucune difficulté.
Re: Puissance fonctionnelle / recurrence
A vrai dire j'ai l'habitude de travailler avec des suites et bien que ça soit plus simple ici, je ne vois pas comment faire
Re: Puissance fonctionnelle / recurrence
Il s'agit de montrer, par récurrence sur  , que pour tout entier naturel
, que pour tout entier naturel  :
:
Pour tout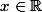 ,
, }(x)= 2^nx)
Initialisation ( cas )
)
Hérédité (hypothèse de récurrence : c'est vrai pour l'entier naturel ; à montrer : c'est vrai pour
; à montrer : c'est vrai pour 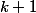 )
)
Pour tout
Initialisation ( cas
Hérédité (hypothèse de récurrence : c'est vrai pour l'entier naturel
Re: Puissance fonctionnelle / recurrence
Oui c'est le moment où il faut montrer que c'est vrai pour k +1 que je bloque!
A moins que ça soit juste : (x) = 2^(k+1) (x) ?)
A moins que ça soit juste :
Re: Puissance fonctionnelle / recurrence
Bonsoir f^(n+1) (x) = f o f^(n)(x) = f( 2^nx) =... je te laisse finir: calcule f(2^nx) et tu auras fini
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
