à propos de (1+rac(2))^n
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marc16
- Messages: 6
- Enregistré le: 01 Nov 2008, 10:19
-
 par marc16 » 02 Nov 2008, 15:00
par marc16 » 02 Nov 2008, 15:00
Bonjour,
Depuis plusieurs jours, je sèche sur l'exercice suivant:
1) Montrer qu'il existe une suite
)
d'entiers tel que:
^{n}=\sqrt{p_{n}}+\sqrt{p_{n}+1})
2) Exprimer
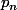
en fonction de n.
La relation marche pour les petites valeurs de n.
Faut-il procéder par récurrence?
Avec le binôme de Newton en distingant les cas n pair, n impair?
mais je n'arrive pas à conclure.
Merci pour vos conseils.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 02 Nov 2008, 15:21
par ThSQ » 02 Nov 2008, 15:21
En fait p_n+1 est le carré d'un entier = a(n)²
Montre qu'on a un truc style a(n+2) = A * a(n+1) + B * a(n) pour A et B que je te laisse trouver ;)
Tu peux aussi regarder du côté de (1 - sqrt(2)) ^n mais ça doit pas être l'esprit de ton exo.
-
mathelot
 par mathelot » 02 Nov 2008, 15:50
par mathelot » 02 Nov 2008, 15:50
Bjr,
une autre piste que celle proposée par ThSQ (salut)
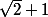
et
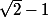
sont deux nombres réels inverses l'un de l'autre.
Avec un peu de quantité conjuguée, on a
nécessairement:
^n - (\sqrt{2}-1)^n \right)}^2)
reste à montrer que cette quantité

a bien les propriétés requises (entier+l'égalité)
-
marc16
- Messages: 6
- Enregistré le: 01 Nov 2008, 10:19
-
 par marc16 » 02 Nov 2008, 16:14
par marc16 » 02 Nov 2008, 16:14
Bonjour,
Merci pour le coup de main mais je n'arrive pas à avancer beaucoup plus
pouvez-vous encore m'éclaircir les idées
merci
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 02 Nov 2008, 16:21
par ThSQ » 02 Nov 2008, 16:21
mathelot a écrit:une autre piste que celle proposée par ThSQ (salut)
Salut à toi aussi moussaillon

C'était ma deuxième suggestion mais vu la deuxième question .....
-
mathelot
 par mathelot » 02 Nov 2008, 16:29
par mathelot » 02 Nov 2008, 16:29
mathelot a écrit:^n - (\sqrt{2}-1)^n \right)}^2)
a)

est un entier naturel, comme on le voit en développant le binome de Newton.
b)
^n - (\sqrt{2}-1)^n =2 \sqrt{pn})
mais:
^n (\sqrt{2}-1)^n = -1)
on connait la somme et le produit de ces nombres.
A quoi ça fait penser ?
à
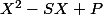
, pas vrai ?
^n)
est la racine positive de

-
mathelot
 par mathelot » 02 Nov 2008, 17:02
par mathelot » 02 Nov 2008, 17:02
ThSQ a écrit:Salut à toi aussi moussaillon

C'était ma deuxième suggestion mais vu la deuxième question .....
j'adoooooore cet exo.
^n - (\sqrt{2}-1)^n}{2} \right)}^2)
))
:zen:
:ptdr: :ptdr:
-
mathelot
 par mathelot » 02 Nov 2008, 17:21
par mathelot » 02 Nov 2008, 17:21
c'est bizarroïde cette intrusion de la trigo
hyperbolique.
j'aurai bien vû débarquer du
 = (\sqrt{2}-1)^2=\frac{\sqrt{2}-1}{\sqrt{2}+1})
-
mathelot
 par mathelot » 02 Nov 2008, 17:33
par mathelot » 02 Nov 2008, 17:33
marc16 a écrit:Bonjour,
Merci pour le coup de main mais je n'arrive pas à avancer beaucoup plus
merci
pose des questions...
ThSQ a écrit:En fait pn est le carré d'un entier = a(n)²
si n est impair ? avec mes formules (exactes) je trouve
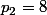
-
marc16
- Messages: 6
- Enregistré le: 01 Nov 2008, 10:19
-
 par marc16 » 02 Nov 2008, 18:26
par marc16 » 02 Nov 2008, 18:26
Merci pour vos lumières, le ciel s'éclaircit même à cette heure!!!
L'expression de p(n) avec rac(2) doit convenir.Je regarde dans le détail si p(n)vérifie les conditions.
-
mathelot
 par mathelot » 02 Nov 2008, 18:44
par mathelot » 02 Nov 2008, 18:44
re,
on a trouvé
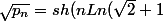))
on pose pour les rangs impairs
 Ln(\sqrt{2}+1)))
ça donne
q1=1,q2=7,q3=41,q4=239,q5=1393,q6=8119
la suite est référencée
[url=http://www.research.att.com/~njas/sequences/?q=1%2C7%2C41%2C239%]içi[/url]
on pose pour les rangs pairs
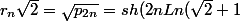))
ça donne
r1=2,r2=12,r3=70,r4=408,r5=2378,r6=13860
là
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 02 Nov 2008, 18:57
par ThSQ » 02 Nov 2008, 18:57
mathelot a écrit:si n est impair ? avec mes formules (exactes) je trouve
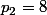
Ouais typo, c'est pn+1 qui est un carré. :marteau:
-
mathelot
 par mathelot » 02 Nov 2008, 19:03
par mathelot » 02 Nov 2008, 19:03
ThSQ a écrit:Ouais typo, c'est pn+1 qui est un carré. :marteau:
d'après mes vérifs,

et

sont des carrés parfaits alternativement.
euh , pour ta récurrence, tu pourrais me donner un indice ? :hum:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 02 Nov 2008, 19:46
par lapras » 02 Nov 2008, 19:46
salut
^n)
En passant au conjugué,
^n)
en sommant :
^n+(1-\sqrt{2})^n)
donc
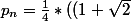^n+(1-\sqrt{2})^n)^2)
Soit a_n une suite d'entiers telle que :


En passant à l'équation caractéristique (si tu ne connais pas, il faut passer par les matrices, ou faire une récurrence inélégante...) :
^n+(1-\sqrt{2})^n)
Par récurrence

est pair
donc
^2)
p_n est donc bien le carré d'un entier
soit


donc

donc
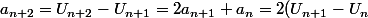+U_n-U_{n-1})
donc

En passant à l'équation caractéristique :
(car
^3-3(1+\sqrt{2})^2+(1+\sqrt{2})+1=0)
)
^n)
Or

d'où le résultat
-
mathelot
 par mathelot » 02 Nov 2008, 20:31
par mathelot » 02 Nov 2008, 20:31
lapras a écrit:^n)
En passant au conjugué,
^n) <--- c'est faux
<--- c'est faux
Lapras, je relève deux erreurs:
a) la formule n'est pas
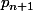
mais

b) on ne passe pas au conjugué mais à l'inverse. Il y a une erreur de signe.
^n)
En passant à l'inverse (puis en conjuguant):
^n)
par contre, la méthode est bien: reconstituer l'équation
caractéristique puis la récurrence.
La formule exacte n'est pas celle que tu as écrite.
lapras a écrit:^2)
p_n est donc bien le carré d'un entier
ben non, on a vu que
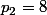
-
mathelot
 par mathelot » 02 Nov 2008, 20:47
par mathelot » 02 Nov 2008, 20:47
Les formules (justes) donnent une réalité plus complexe:
^n=\sqrt{p_n}+\sqrt{1+p_n})
si n est impair ,

est un carré parfait
au rang suivant,c'est

qui est un carré parfait:
^1=\sqrt{1}+\sqrt{2})
^2=\sqrt{8}+\sqrt{9})
^3=\sqrt{49}+\sqrt{50})
^4=\sqrt{288}+\sqrt{289})
pour les enseignants de collège qui nous lisent,
merveilleuses vérifications à faire faire aux élèves de troisième !
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 02 Nov 2008, 21:01
par lapras » 02 Nov 2008, 21:01
Alors j'ai mal lu l'énoncé !
J'ai lu

...
Ce qui change tout avec

Mon erreur de signe change toute ma démonstration apprement ! :marteau:
-
mathelot
 par mathelot » 02 Nov 2008, 21:12
par mathelot » 02 Nov 2008, 21:12
mathelot a écrit:^4=\sqrt{288}+\sqrt{289})
pour les enseignants de collège qui nous lisent,
merveilleuses vérifications à faire faire aux élèves de troisième !
En classe de troisième, tu fais développer
^2 \right)^2)
deux fois avec l'identité
^2)
et simplifier la somme

qui comporte deux entiers avec des facteurs carrés.
et tu conclues avec la transitivité de l'égalité.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Nov 2008, 22:05
par yos » 02 Nov 2008, 22:05
Bonjour à vous tous.
Je voulais apporter un point de vue qui est pas forcément dans ce qui précède :
^n=a_n+b_n\sqrt2)
avec

et

entiers.
On montre aisément que
^n=a_n-b_n\sqrt2)
avec les mêmes entiers

et

.
En multipliant membre à membre, on trouve
^n=a_n^2-2b_n^2)
,
Donc en posant
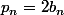
ou
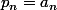
selon la parité de n, on a la relation voulue.
Les entiers

et

se calculent explicitement donc

aussi.
-
mathelot
 par mathelot » 02 Nov 2008, 22:37
par mathelot » 02 Nov 2008, 22:37
yos a écrit:Donc en posant
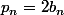
ou
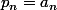
selon la parité de n, on a la relation voulue.
Les entiers

et

se calculent explicitement donc

aussi.
euh,

ou

mais qu'est-ce qu'ils ont tous ce soir ? :doh: :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
