Projection

[sandrine_guillerme]

Bijour tout le monde !

une petite question dans un problème sur lequel je bug depuis un moment :

f : R^n -> R
j'aimerais montrer que le graphe de la différentielle de f cà d l'ensemble de points (x,p) avec p élèment de de la différentielle de x est fermé ..

Hypothèse: f est convexe

je voulais utiliser le théorème du graphe fermé .. mais ça bug

D'avance merci :we:

[maf]

Je crois voir pkoi le th. du graphe fermé ne marche pas ...

f continue ssi le graphe et fermé (mais pas réciproque forcément)

Par contre, je réfléchis pour ton problème

[sandrine_guillerme]

Exactement ..

et merci d'avance maf :we:

[sandrine_guillerme]

Je me demande si le sup de tous les p qui sont dans la diff de f(x) est fini.. juste une question comme ça... (comme je l'ai dis ailleurs)

je le vois bien dans un dessin, si ça peut nous aider ?

[tize]

Bonjour Sandrine,
je ne comprends pas ceci :

...càd l'ensemble de points (x,p) avec p élément de la différentielle de x...

Que veut dire différentielle de x ? x est une application ?
Que veut dire "p élément de la différentielle" ? C'est quoi un élément d'une différentielle ? Pour moi une différentielle est une application linéaire et continue... :hein:

[sandrine_guillerme]

bijour José :we:

excuses moi je me suis très mal exprimée

p df(x)

d : dérivée partielle
donc j'aimerais montrer que le graphe de d(f) est fermé

(lire d comme déron :zen: )

[tize]

Il me semble bien que le graphe d'une application linéaire entre deux evn de dimensions finies (qui sont donc des Banach) est toujours fermé...non?

[sandrine_guillerme]

Ah, ça serait trop beau ! ça m'arrangerait en fait !



sinon moi je savais pas ce truc


as tu une démo stp ?

[tize]

Ça n'est rien d'autre que le théorème du graphe fermé en dimension finie, puisque est complet pour tout entier et une application linéaire en dimension finie est toujours continue...

[sandrine_guillerme]

Il me semble bien que le graphe d'une application linéaire entre deux evn de dimensions finies (qui sont donc des Banach) est toujours fermé...non?

Sinon il faut l'hypothèse de continuité, qui n'a pas l'air de poser un problème car il s'agit d'un evn de dim fini

je crois que c'est une bonne idée ..
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_du_graphe_ferm%C3%A9

[sandrine_guillerme]

Bien vu josé,

j'enchaîne donc, mon prof nous a parlé de dérivablité au sens de Gâteaux voilà donc la question essentielle de cet exo ,

Montrer que si f est dérivable au sens de Gâteaux alors f est de C^1

[sandrine_guillerme]

On n'a encore utilisé ni le fait que f est convexe,
ni la remarque que le prof a dit rapidement :

pour tout r > 0
sup {|p|, p df ; |x| r } <
mais alors là je ne vois pas vraiment comment montrer cette assertion qui m'a l'air vraiment intuitive pour n = 2

[tize]

Désolé mais je ne comprends toujours pas ça : ; df est une application linéaire, pas un ensemble; pour moi ça ne veut rien dire : p "appartient" à l'application linéaire. Ou tu veux dire p est dans l'image de B(x,r) par l'application linéaire df ?

[sandrine_guillerme]

Désolée josé,
c'est encore une erreur de frappe ..
elle est là la question
montrer que pour tout r > 0
sup {|p|, p df(x) ; |x| r } <

ça va mieux là?

[sandrine_guillerme]

J'ai eu un indice dans un autre endroit

on m'a dis :

Si est dans le sous-différentiel de en on a pour tout , puisqu on a un produit scalaire avec ..

mais ça ne m'avance pas du tout ,

est ce que la question est vraiment dure ?

[tize]

Donc si j'ai bien compris tes notations, signifie que p est une dérivée directionnelle de f, c'est ça ?
En rapport avec ça ?

[sandrine_guillerme]

tout à fait José,

et d'ailleurs merci pour le lien !

[sandrine_guillerme]

Je récapitule pour ceux qui n'ont pas tout suivi et qui n'ont pas envie de tout lire,

f : R^n -> R convexe ,

Montrer que pour tout r > 0
sup {|p|, p df ; |x| r } <

[tize]

Salut,
peut être une idée...car en réalité je ne suis toujours pas sur d'avoir compris tes notations...
Je prends ; cela veut dire (si j'ai bien compris ce que p représente) qu'il existe une direction telle qu'en notant pour 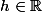la fonction admette en 0 la dérivée ...
Déjà on peut remarquer que est convexe en effet : pour ,
On a donc pour cette fonction convexe : avec :

Soit en prenant et en faisant tendre :
(il est possible de minorer aussi de la même manière...) et puisque la fonction est continue, il est possible de majorer le membre de droite par une constante sur

[sandrine_guillerme]

Voilà, c'est ça !
bravo José !

moi je me suis dis que fonction convexe implique localement lipschitzienne, ce qui prouve à la fois, l'existence du sup, et qu'il soit fini !

merci beaucoup José, merci beaucoup !