Problème sur les suites
21 messages
- Page 1 sur 2 - 1, 2
Problème sur les suites
Bonjour
je cale sur cette question:
Soit Un définie par u0 >0 , u1 > 0 et quelque soit n appartenant à N
Un+2 = racine carré Un + Un+1
Montrer que pour tout n appartenant à N , Un > 0
Merci
je cale sur cette question:
Soit Un définie par u0 >0 , u1 > 0 et quelque soit n appartenant à N
Un+2 = racine carré Un + Un+1
Montrer que pour tout n appartenant à N , Un > 0
Merci
thedream01 a écrit:Comme l'a déja dit gol_de_grosso, tu fais une récurrence!
Tu supposes que quelque soit k de 0 à n-1, u(k)>0.
Donc u(n-1)+u(n-2) est positif par hypothése..donc u(n)= (u(n-1)+u(n-2))^(1/2) existe et est >0..
merci de répondre si vite, mais j'ai du mal à comprendre, il faut dire que les suites c'est un de mes points faibles
Le principe de la récurrence :
tu as à montrer une propriété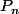 pour tout entier n (par exemple :
pour tout entier n (par exemple :  , ou bien
, ou bien }{2}) ).
).
1)Tu montres que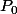 est vraie.
est vraie.
2)Tu supposes que pour fixé quelconque, si
fixé quelconque, si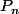 est vraie, alors
est vraie, alors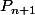 est vraie.
est vraie.
Ta propriété est alors montrée : si tu prends n=0, tu en déduis que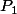 est vraie, puis avec n=1, que
est vraie, puis avec n=1, que  est vraie, et ainsi de suite pour tout n.
est vraie, et ainsi de suite pour tout n.
Le point important à comprendre dans le raisonnement est que n est fixé quelconque dans ...
...
La variante du raisonnement par récurrence faite ici est à l'étape 2) : ici, tu dois prendre plutôt :
2bis) Tu suppose que pour n fixé quelconque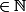 , on a :
, on a :  est vraie.
est vraie.
Ca ne change rien théoriquement, mais pratiquement c'est plus pratique dans plusieurs cas (dans le tien en particulier). C'est ce qu'on appelle une récurrence forte.
tu as à montrer une propriété
1)Tu montres que
2)Tu supposes que pour
Ta propriété est alors montrée : si tu prends n=0, tu en déduis que
Le point important à comprendre dans le raisonnement est que n est fixé quelconque dans
La variante du raisonnement par récurrence faite ici est à l'étape 2) : ici, tu dois prendre plutôt :
2bis) Tu suppose que pour n fixé quelconque
Ca ne change rien théoriquement, mais pratiquement c'est plus pratique dans plusieurs cas (dans le tien en particulier). C'est ce qu'on appelle une récurrence forte.
Je tiens à dire que je ne réponds pas aux messages privés qu'on m'envoie sur ce genre de sujet.
Pour en revenir au problème...
D'après l'hypothèse de récurrence,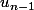 et
et 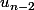 sont positifs. Une somme de nombres positifs est positive...
sont positifs. Une somme de nombres positifs est positive...
Parce que la racine carrée d'un nombre positif existe bien, et est positive...
Il serait bon de revoir des connaissances de calcul de base (niveau seconde environ) !!
Pour en revenir au problème...
"basket" a écrit:Tu supposes que quelque soit k de 0 à n-1, u(k)>0.
Donc u(n-1)+u(n-2) est positif par hypothése..donc
u(n)= (u(n-1)+u(n-2))^(1/2) existe et est >0..
je ne vois pas
pourquoi u(n-1)+u(n-2) est positif
D'après l'hypothèse de récurrence,
et pourquoi u(n)= (u(n-1)+u(n-2))^(1/2) existe et est >0..
Parce que la racine carrée d'un nombre positif existe bien, et est positive...
Il serait bon de revoir des connaissances de calcul de base (niveau seconde environ) !!
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
