Problème d'intégration...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 19 Mai 2008, 13:09
par skysurf3000 » 19 Mai 2008, 13:09
Mon problème :
calculer
, \mathrm dt)
Avec l'intégration par partie on se retrouve toujours soit avec un cos, soit avec un sin, donc ça m'arrange pas... :mur:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 19 Mai 2008, 13:25
par ffpower » 19 Mai 2008, 13:25
je suis pas sur que cette integrale soit calculable..
-
Baltha
- Membre Relatif
- Messages: 114
- Enregistré le: 03 Nov 2007, 12:53
-
 par Baltha » 19 Mai 2008, 13:52
par Baltha » 19 Mai 2008, 13:52
Je pense qu'on peut s'en sortir en réalisant une double intégration par partie

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 19 Mai 2008, 15:06
par fatal_error » 19 Mai 2008, 15:06
Bonjour,
avec le changement de variable
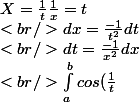dt=\int_a^b cos(x) \frac{-1}{x^2}dx\\<br />=[cos(x)\frac{1}{x}]_a^b+\int_a^b \frac{sin(x)}{x}dx)
la deuxieme intégrale s'appèle Si(x):
son dvpt en seriela vie est une fête

-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 19 Mai 2008, 15:29
par ffpower » 19 Mai 2008, 15:29
bien vu..c est donc maintenant sur qu il n ya pas de formule en tout cas
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités