Problème d'inégalité complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 16 Fév 2014, 01:46
par savan-306D » 16 Fév 2014, 01:46
Salut, j'ai un problème d'inégalité de complexes :
on a

j'ai montré grâce à un changement d'indice du Sigma que :
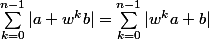
en posant

et je dois en déduire que

j'ai essayé de commencer par montrer que quel que soit k inférieur à n :

puis faire la somme mais la relation est fausse j'ai trouvé un contre exemple par calcul : n=10 k=5 a=2+i b=3+i
j'attends vos idées ..
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 16 Fév 2014, 15:32
par jlb » 16 Fév 2014, 15:32
salut, inégalité triangulaire à partir des expressions égales + factorisation pat |1+w^k| + une minoration par les n/2 premiers termes de la somme. Cela doit te donner ton inégalités, je crois.
j'attends vos idées ..
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 16 Fév 2014, 16:23
par savan-306D » 16 Fév 2014, 16:23
J'ai pas très bien compris ton raisonnement, 'inégalité triangulaire à partir des expressions égales'
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 16 Fév 2014, 16:36
par jlb » 16 Fév 2014, 16:36
savan-306D a écrit:J'ai pas très bien compris ton raisonnement, 'inégalité triangulaire à partir des expressions égales'
ne tiens pas compte du message, désolé, c'était une mauvaise piste.
par contre pour n pair, en utilisant |u+v|+|u-v|>|u|+|v| on doit obtenir l'inégalité si je n'ai pas commis une autre bourde. (u=a et v=w^k.b)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Fév 2014, 12:14
par Ben314 » 17 Fév 2014, 12:14
Salut,
Si

est non nul et que l'on écrit

alors on a :
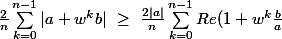\ <br />=\ \frac{2|a|}{n}\sum_{k=0}^{n-1}\Big(1+\cos(\frac{2k\pi}{n})\alpha-\sin(\frac{2k\pi}{n})\beta\big))
Or, comme

, on a
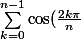=\sum_{k=0}^{n-1}\sin(\frac{2k\pi}{n})=0\)
et donc

qui est
 à condition que
à condition que 
, or grâce à la question précédente, on peut échanger les rôles de

et de

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 17 Fév 2014, 16:46
par jlb » 17 Fév 2014, 16:46
merci, pour cette réponse complète! je ne suis pas l'auteur de la question mais j'ai bien tourné en rond pour aboutir à pas grand chose.
-
savan-306D
- Membre Naturel
- Messages: 64
- Enregistré le: 24 Nov 2013, 23:39
-
 par savan-306D » 20 Fév 2014, 23:37
par savan-306D » 20 Fév 2014, 23:37
Oui merci en fait pour la rédaction
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
