Bonsoir besoin d'aide s'il vous plait .
Exercice :
Une firme pharmaceutique souhaite lancer sur le marché d’un pays africain un préservatif
féminin. Une étude économique a montré que le lancement de ce préservatif ne pouvait être
rentable que s’il y avait au moins 20% d’acheteurs potentiels. Un sondage sur 1600 femmes ?
sexuellement actives a monté que 192 sont favorables au préservatif féminin. Avec un risque
d’erreur de 2,5%, quelle décision conseilleriez-vous à la firme pharmaceutique ? Justifier votre
réponse
Probabilité et statistiques
8 messages
- Page 1 sur 1
Re: Probabilité et statistiques
Intervalle de fluctuation asymptotique au seuil de 5% -> on prend -1.96 et 1.96
il faut changer ces deux valeurs pour 2.5% (sauf si tu travailles en unilatéral, ce qui est possible ici).
il faut changer ces deux valeurs pour 2.5% (sauf si tu travailles en unilatéral, ce qui est possible ici).
Re: Probabilité et statistiques
[si quelqu'un peut confirmer mes calculs, je suis novice en statistique paramétrique]
On estime la proportion d'acheteurs potentiels, qui est notre paramètre .
.
On veut tester l'hypothèse nulle : contre l'hypothèse alternative
contre l'hypothèse alternative 
Moyenne empirique sur l'échantillon=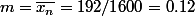
Il est naturel de procéder au rejet de l'hypothèse nulle si , où la valeur c vérifie
, où la valeur c vérifie =\alpha)
Sous l'hypothèse nulle, on fait l'approximation normale, c'est à dire que}{1600}}}=40 \times \frac{\bar{X_n}-p}{\sqrt{p(1-p)}}) suit la loi normale centrée réduite
suit la loi normale centrée réduite
donc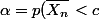=p(40 \times \frac{\bar{X_n}-p}{\sqrt{p(1-p)}}<40 \times \frac{c-p}{\sqrt{p(1-p)}})=p(Z<40 \times \frac{c-p}{\sqrt{p(1-p)}})) où
où  suit la loi normale centrée réduite
suit la loi normale centrée réduite
On remarque qu'ici cela se simplifie et finalement) suit la loi normale centrée réduite
suit la loi normale centrée réduite
Pour un niveau de confiance 95%, niveau de risque alpha=5%, on obtient un quantile de -1.64 (attention c'est unilatéral, le -1.96 correspond à un test bilatéral)
Pour un niveau de confiance 97.5%, niveau de risque alpha=2.5%, on obtient un quantile de -1.96
donc pour alpha=2.5%, c est déterminé par l'équation}}=-1.96) soit
soit =-1.96) d'où c=0.1804
d'où c=0.1804
On rejette donc l'hypothèse nulle ici car 0.12<0.1804.
Décision : il y a statistiquement moins que 20% d'acheteurs potentiels.
Conclusion - discussion :
- "favorable au préservatif féminin" et "acheteur potentiel" : pas pareil, cela dépend sûrement du prix et des politiques publiques (contraception, éducation des femmes etc)
- on peut imaginer une politique de subventions qui enlèverait (ou ferait baisser) la contrainte de 20% d'acheteurs potentiels pour la rentabilité qui dépend aussi du prix d'achat (base de l'économie : recette=quantité*prix)
On estime la proportion d'acheteurs potentiels, qui est notre paramètre
On veut tester l'hypothèse nulle :
Moyenne empirique sur l'échantillon=
Il est naturel de procéder au rejet de l'hypothèse nulle si
Sous l'hypothèse nulle, on fait l'approximation normale, c'est à dire que
donc
On remarque qu'ici cela se simplifie et finalement
Pour un niveau de confiance 95%, niveau de risque alpha=5%, on obtient un quantile de -1.64 (attention c'est unilatéral, le -1.96 correspond à un test bilatéral)
Pour un niveau de confiance 97.5%, niveau de risque alpha=2.5%, on obtient un quantile de -1.96
donc pour alpha=2.5%, c est déterminé par l'équation
On rejette donc l'hypothèse nulle ici car 0.12<0.1804.
Décision : il y a statistiquement moins que 20% d'acheteurs potentiels.
Conclusion - discussion :
- "favorable au préservatif féminin" et "acheteur potentiel" : pas pareil, cela dépend sûrement du prix et des politiques publiques (contraception, éducation des femmes etc)
- on peut imaginer une politique de subventions qui enlèverait (ou ferait baisser) la contrainte de 20% d'acheteurs potentiels pour la rentabilité qui dépend aussi du prix d'achat (base de l'économie : recette=quantité*prix)
Re: Probabilité et statistiques
oui, j'avais supposé que l'unilatéral était mieux ici (uα de 5% symétrique et 2.5% unilatéral sont les mêmes en fait)
NB : avec une approximation de base, f+1/sqrt(n) << 0.2, c'est rejeté
NB : avec une approximation de base, f+1/sqrt(n) << 0.2, c'est rejeté
Re: Probabilité et statistiques
Merci pour votre aide j'aimerais avoir quelques documents qui pourraient me servir
Merci bien encore
Merci bien encore
Re: Probabilité et statistiques
Pour LB2
Xnbarre-0.2 ne suit pas une loi normale, mais pas centrée (problème de biais)
Xnbarre-Xbarre où Xbarre est la vraie valeur sur la population (inconnue) suit une loi normale et centrée.
On doit donc modifier la façon dont on explique
-> on peut partir d'une distribution théorique centrée sur 0.2 et on vérifie si l'échantillon correspond à la théorie.
-> on peut partir de l'échantillon, et parler de fluctuation.
Xnbarre-0.2 ne suit pas une loi normale, mais pas centrée (problème de biais)
Xnbarre-Xbarre où Xbarre est la vraie valeur sur la population (inconnue) suit une loi normale et centrée.
On doit donc modifier la façon dont on explique
-> on peut partir d'une distribution théorique centrée sur 0.2 et on vérifie si l'échantillon correspond à la théorie.
-> on peut partir de l'échantillon, et parler de fluctuation.
Re: Probabilité et statistiques
@pascal16 oui je parlais sous réserve de l'hypothèse nulle, c'est ç dire que X barre=0.2
Effectivement je suis d'accord avec ce qui suit (et j'ai toujours un problème entre minuscules et majuscules)
Effectivement je suis d'accord avec ce qui suit (et j'ai toujours un problème entre minuscules et majuscules)
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
