Probabilité et mesure

[mariounette]

Bonjour,

Est-ce que quelqu'un pourrait me donner le critère de caractérisation des mesures please? merci.

[BQss]

Bonjour,

Est-ce que quelqu'un pourrait me donner le critère de caractérisation des mesures please? merci.

Salut

Le critère le plus "axiomatique" c'est:

Avec l et m deux mesures sur (E, ) et C une classe de partie de E vérifiant:

1)La tribu engendrée par C est

2)l(A)=m(A)< pour tout

3)C est stable par intersection finie.

4) Il existe une suite croissante de C tel que

Alors m et l sont égales.

Mais maintenant tu as plein d'autres caracterisations de mesure dont on se sert plus allegrement en probabilité tel que l'égalité des transformées de fouriée(fonction caracteristique), l'égalité des transformée de la Laplace(pour les variables positives) ou l'égalité des fonctions génératrices pour les variables discrètes ou encore evidemment l'égalité des densités.

[BQss]

Peut-etre que j'ai pas exactement saisi ta question, si tu voulais simplement la definition d'une mesure:

une mesure m sur (E,) est une application de dans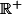

vérifiant:

la -additivité: mesure de l'union d'ensemble est égale a la somme de la mesure des ensembles pour toute suite d'ensemble deux a deux disjoints.

la mesure de l'ensemble vide est nulle.


Pour une probabilité on rajoute que la mesure de E vaut 1... En découle un grand nombre de propriétés sympathiques.

[mariounette]

Non je ne te demandais pas la def mais le critère tu avais bien compris.
Le truc c ke j ai un exo ki te montre kune fonction de repartition tu peux la decomposer en une partie atomique une partie densité et une partie étrangère. La premiere question t exprime la fonction de repartition comme l integrale d une fonction g integrable, ce ki pour moi veut dire que g est la densité de probabilité. Mais pour affirmer ceci il est demandé d'utiliser le critère de caractérisation des mesures et le critère que tu m as donné je le connais mais je voyais pas trop le rapport. En même temps j y ai pas trop réfléchi encore, je vais me pencher dessus.

Merci pour ta réponse.

[BQss]

g n'est pas forcement la densité de probabilité si g est infinie a certains endroit(en certains points), la mesure qui en decoule ne sera alors pas absolument continue par rapport a la mesure de Lebesgue.

Est ce que ton integrale se fait par rapport a la mesure de Lebesgue partout ou y a -t-il quelquechose comme de a à b exclu on integre fdx, puis en b, un nombre y (apartenant à [0;1] ) fois la mesure de dirac en b (y étant alors la hauteur du saut) puis integrale de b exclu a c de gdx.

Dans tout les cas, si non pour revenir a la question de l'exo, tu peux te servir de la fonction de repartition pour carateriser une mesure. En effet la classe des fermés engendre la tribu borelienne et tu peux appliquer le theoreme en posant

Avec F et G deux fonctions de repartition en appliquant le theoreme fondamental, le fait que F(t)=G(t) pour tout t, entraine l'égalité des mesures et donc que les variables aléatoires qui en decoulent ont les memes lois de probabilité.

[mariounette]

Question purement existencielle :

Une mesure mu est absolument continue par rapport à une autre mesure nu si elle admet une densité par rapport à nu. Je comprend la terminologie continue mais je sais d'où sort le terme absolument? Tu as une idée?

[BQss]

C'est lié a la définition de la continuité absolue pour des fonctions (ou la valeur absolue intervient, comme pour la "convergence absolue" par exemple) qui est intimement lié a cette notion.
Une mesure dérivant d'une fonction de répartition F est absolument continue par rapport a une autre mesure ssi sa fonction de repartition est localement absolument continue.
En gros ca veut dire que ta fonction de répartition n'a pas de sauts de discontinuité (ils correspondent à des points de densités infini).

un lien ici.
http://fr.wikipedia.org/wiki/Absolue_continuit%C3%A9

[mariounette]

Non mais si ma fonction est continue c'est bien qu'elle n'est pas discontinue et donc qu'elle n'admet pas de points de discontinuité. Maintenant le absolue dans continuité absolue veut dire que ta fonction est à variation bornée, à mon avis.

[HAL 9000]

l'absolue continuité est en rapport avec l'integration :

On dit que F est une fonction absolument continue sur l'intervalle [a,b] si il existe une fonction f intégrable sur [a,b] telle que pour tout x de [a,b] :



Evidemment, une fonction absolument continue est continue...