Probabilité combinaison pondérée.

[Gladolfera]

Bonjour.
Essayant de faire joujou avec les probabilités presque 10 après avoir arrêté les maths, je me suis remis un peu à niveau grâce au net, mais je me trouve malgré-tout dans une impasse.

Voici le contexte :
Je dispose d'un dés à 6 face, avec 4 faces identiques 2 à 2 (en gros un dés avec 1,1,2,2,3,4).

Pour calculer le nombre de combinaisons (l'ordre ne m'intéresse pas) j'ai l'impression que la bonne approche est de supposer que je fais un tirage de 6 éléments parmi 4 avec répétition (je pense avoir validé mon hypothèse avec un petit programme informatique qui fait des boucles).

En revanche pour calculer la probabilité de chaque combinaison j'ai plus de mal à avoir un résultat cohérent :

Sachant que pour un tirage de k parmi n, le nombre de combinaison se trouve en divisant le nombre d'arrangement par k!, je pensais qu'il me suffisait de calculer la proba d'un arrangement correspondant à la combinaison, puis de la multiplier par k!.

En d'autres termes, je pensais calculer la proba de cette combinaison : 433221 en faisait :
P(1)*P(2)*P(2)*P(3)*P(3)*P(4)*6! = 1/3*1/3*1/3*1/6*1/6*1/6*6!

Cependant, lorsque j'additionne les probas de toutes les combinaisons possibles, je ne trouve pas 1.
Mon approche est-elle erronée ?
Je pensais trouver plus de réponses sur ce cas sur le net, mais ce n'est apparemment pas une situation si rependue que ça :livre:

Pourriez-vous m'aider ?

Merci d'avance !

Glad !

[Ben314]

Je suis pas sûr d'avoir tout capté (en particulier ton dés avec "4 faces identiques 2 à 2" qui serait 1,1,2,2,3,4), mais ton truc ressemble plus que fortement à une loi multinationale :

Loi multinationale (généralisation de la loi binomiale) :
On effectue n tirages indépendants d'un même truc ayant k résultats différentes de proba respectives (dont la somme fait 1).
On note les variables aléatoires comptant le nombre de fois qu'on a obtenue le résultat 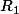, le nombre de fois qu'on a obtenue le résultat 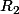,... (on a donc forcément )

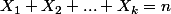Alors, si on se donne des entiers dont la somme fait n, la proba que est :
où (appelé "coefficient multinational)

Dans le cas k=2, c'est la loi binomiale.

Dans ton exemple (si je comprend bien), il y a 4 résultats possibles ("1", "2", "3" et "4") de proba respectives et tu veut la proba. qu'en faisant n=6 tirage, tu ait (dans un ordre quelconque) 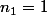fois "1", 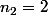fois "2", 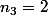fois "3", 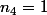fois "4".
TU applique la formule ça dessus et tu as le résultat (c'est pas archi dur à démontrer...)

[Gladolfera]

Plop !
Merci beaucoup pour la réponse rapide !
Les mécanismes qui gèrent ce calcul m'échappent, mais en appliquant la formule à la lettre ça fonctionne très bien, et ça se décline impeccablement dans mon petit programme informatique !

Merci encore ! :++:

Gladolfera

[Ben314]

En fait, tu était trés proche du résultat, mais c'est ton "factorielle 6" qui n'allait pas.
6!, ça serait le nombre de façon de "ranger" 6 symboles différents or toi, avec ton 433221, les 6 symboles ne sont pas différents.
Pour voir comment y remédier (et d'où sortent les fameux coefficients multinationaux), il sufit de te dire que si tu différenciait les deux "3" (par exemple en en écrivant un en rouge et l'autre en bleu) et aussi les deux "2" (idem), là, il y aurait bien 6! façons de les ranger.
Or, si tu part d'un "rangement" non colorié, il y a 2! façons de colorier les deux "2" et 2! façons de colorier les deux "3" donc partant d'une solution "non colorié", il y a 2!x2! façons de la colorié.
Donc le nombre de solutions "non coloriées" est 6!/(2!x2!)

Evidement, de même, si tu voulais 3 fois le "1", 4 fois le "2", 4 fois le "3" et 2 fois le "4", donc avec 3+4+4+2=13 tirages, il faudrait diviser 13! par 3!x4!x4!x2! ce qui est bien la définition du coef. multinational.

P.S. J'ai modifié mon post précédent : je m'était gourré sur la façon dont on note les coeff. multinationaux : le n est en haut et les n_i en bas (enfin bon, ça change pas le résultat...)