Proba - Révision (5)

[barbu23]

Bonjour à tous,

J'ai un autre exercice relativement long que je préfère le faire avec vous, le voiçi :

Exercice :
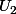
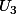
Un joueur dispose d'un dé cubique bien équilibré, dont les faces sont numérotés de à , et de urnes, , et contenant chacune boules, où : .
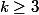
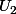
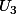
Il y'a boules noires dans , et deux boules noires dans , et une boule noire dans . Toutes les autres boules dans les urnes sont blanches. Les boules sont indiscernables au toucher.

Une partie de déroule de la manière suivante : Le joueur lance le dé.
- S'il obtient le numéro , il prend au hasard une boule dans l'urne , note sa couleur et la remet dans .
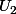
- S'il obtient un multiple de , il prend au hasard une boule dans , note sa couleur et la remet dans .
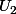
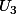
- Si le numéro amené par le dé n'est ni , ni un multiple de , il prend au hasard une boule dans , note sa couleur, et la remet dans l'urne .

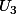
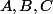
On désigne par et les événements suivants :
- = Le dé amène le numéro
- = Le dé amène un multiple de
- = Le dé amène un numéro qui n'est ni , ni un multiple de
- = La boule tirée est noire.

Le joueur joue une partie :
Montrer que la probabilité qu'il obtienne une boule noire est égale à .
Calculer la probabilité que le dé ait amené le sachant que le boule tirée est noire.
Déterminer pour que la probabilité d'obtenir une boule noire soit supérieure ou égale à
Déterminer pour que la probabilité d'obtenir une boule noire soit égale à
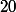
Dans cette question, est choisi pour que la probabilité d'obtenir une boule noire en jouant une partie soit égale à . Le joueur fait parties. indépendantes les unes des autres, Calculer, la probabilité qu'il obtienne au moins une fois une boule noire.

Merci d'avance pour votre aide.

[barbu23]

Svp, j'ai besoin de votre aide. Je n'arrive pas à faire la première question. :happy3:

[BiancoAngelo]

Salut barbu,
Alors, tu fais simplement un arbre pondéré.
Sachant que tu fais les probabilités totales.
Ça.donne 1/6 x 3/k +...

[zaidoun]

la probabilité d'obtenir une boule noire est égale à

[barbu23]

Merci à vous deux pour vos réponses. :happy3:
En fait si j'applique la méthode de l'arbre pondéré, je trouve ceci :




Mais comment trouver : et , par exemple ? C'est la présence du dé dans cette expérience qui m'empêche d'avancer, car je ne sais pas à quel moment il intervient dans le calcul.
Il me semble qu'il faut aussi appliquer la méthode de l'arbre pondéré à l'événement .
C'est à dire : , et c'est à ce moment là qu'intervient la présence du dé dans cette expérience, mais je ne sais pas si je suis sur la bonne voix.
Merci d'avance.

[barbu23]

Merci à vous deux pour vos réponses. :happy3:
En fait si j'applique la méthode de l'arbre pondéré, je trouve ceci :




Mais comment trouver : et , par exemple ? C'est la présence du dé dans cette expérience qui m'empêche d'avancer, car je ne sais pas à quel moment il intervient dans le calcul.
Il me semble qu'il faut aussi appliquer la méthode de l'arbre pondéré à l'événement .
C'est à dire : , et c'est à ce moment là qu'intervient la présence du dé dans cette expérience, mais je ne sais pas si je suis sur la bonne voix.
Merci d'avance.

[barbu23]

Merci à vous deux pour vos réponses. :happy3:
En fait si j'applique la méthode de l'arbre pondéré, je trouve ceci :




Mais comment trouver : et , par exemple ? C'est la présence du dé dans cette expérience qui m'empêche d'avancer, car je ne sais pas à quel moment il intervient dans le calcul.
Il me semble qu'il faut aussi appliquer la méthode de l'arbre pondéré à l'événement .
C'est à dire : , et c'est à ce moment là qu'intervient la présence du dé dans cette expérience, mais je ne sais pas si je suis sur la bonne voix.
Merci d'avance.

[zaidoun]

ici le tirage de boules est lié au résultat de lancement de dé, par exemple pour la première : c'est la probabilité d'obtenir 1 lors de lancement de dé (qui est égale à 1/6) multipliée par la probabilité d'obtenir une boule noire de U_1 (qui est égale à 3/k)

[barbu23]

ici le tirage de boules est lié au résultat de lancement de dé, par exemple pour la première : c'est la probabilité d'obtenir 1 lors de lancement de dé (qui est égale à 1/6) multipliée par la probabilité d'obtenir une boule noire de U_1 (qui est égale à 3/k)

Merci, j'ai compris. :happy3:

[BiancoAngelo]

Merci à vous deux pour vos réponses. :happy3:
En fait si j'applique la méthode de l'arbre pondéré, je trouve ceci :




Mais comment trouver : et , par exemple ? C'est la présence du dé dans cette expérience qui m'empêche d'avancer, car je ne sais pas à quel moment il intervient dans le calcul.
Il me semble qu'il faut aussi appliquer la méthode de l'arbre pondéré à l'événement .
C'est à dire : , et c'est à ce moment là qu'intervient la présence du dé dans cette expérience, mais je ne sais pas si je suis sur la bonne voix.
Merci d'avance.

Tu pourrais ecrire ca directement. Cest le produit des probabilités sur les branches, appelé loi des probabilités totales.
Vu que l arbre contient les evenements qui forment les partitions de l univers.

[barbu23]

Merci. :lol3:
Le reste est facile à faire. Je ne vais pas mettre ici ce que j'ai trouvé dans mon brouillon, parce que j'ai un peu la flemme. :happy3: