Bonsoir à tous :
Voiçi un exo qui me pose quelques problèmes :
Pour réaliser une loterie, un organisateur dispose d'un sac contenant exactement un jeton blanc et

jetons noirs indiscernables au toucher et d'autre part, d'un dé cubique équilibré dont les faces sont numérotés de

à

.
Il décide des règles suivantes pour le déroulement d'une partie :
Le joueur doit tirer un jeton puis jeter le dé :
- Si le jeton est blanc, le joueur perd lorsque le jet du dé donne

.
- Si le jeton est noir, le joueur gagne lorsque le jet du dé donne

.
A la fin de la partie, le jeton est remis dans le sac.
On note

l'événement "Le jeton tiré est blanc", et

l'événement "Le joueur gagne le jeu",
Partie 1 :)
- Montrer que
 = \dfrac{7}{30})
. On pourra s'aider d'un arbre pondéré.
)
- Quelle est la probabilité que le joueur ait tiré le jeton blanc sachant qu'il a perdu ?
)
- Un joueur fait

parties de façon indépendante, Calculer la probabilité qu'il gagne exactement deux, et en donner une valeur approchée à
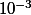
près.
Partie 2 :L'organisateur décide de faire de sa loterie un jeu d'argent :
- Chaque joueur paye 1 Euro par partie.
- Si le joueur gagne la partie, il reçoit 5 Euros.
- Si le joueur perd la partie, il ne reçoit rien.
On note

la variable aléatoire égale au gain algébrique ( positif ou négatif ) du joueur à l'issue d'une partie.
)
Donner la loi de probabilité de

et son espérance mathématique.
)
L'organisateur décide de modifier le nombre

de jetons noirs (
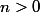
), tout en gardant un seul jeton blanc, Pour quelles valeurs de

le joueur est - il défavorable à l'organisateur ?
Merci d'avance pour votre aide. :happy3:
