Bonjour,
j'aimerais avoir un petit aide sur un exercice de WIMS ayant comme intitulé :
On considère la fonction f, définie par f(x) = 2x² + 16 / 3x² + 48X + 197. On se propose de calculer l'intégrale I= ∫²1(en bas) f(x)dx .
Etape 3 :
En effet F, définie par F(x)= 1/3 ln(3x² +48x+197) est bien une primitive de f sur R .
On en déduit que:
I= ...
Le problème est que qu'en je trouve un résultat sur I=, Wims me compte faux car il veut un résultat en Log (...)-Log(...)
Merci d'avance pour votre aide
Primitives des fonctions usuelles WIMS
6 messages
- Page 1 sur 1
Re: Primitives des fonctions usuelles WIMS
kaolinoui a écrit:Bonjour,
j'aimerais avoir un petit aide sur un exercice de WIMS ayant comme intitulé :
On considère la fonction f, définie par f(x) = 2x² + 16 / 3x² + 48X + 197.
Il manque des parenthèses et il y a une erreur d'exposant au numérateur:
f(x) = (2x + 16) /( 3x² + 48x + 197)
Re: Primitives des fonctions usuelles WIMS
Il y a une erreur d'énoncé ... ou de réponse.
Si f(x) = (2x+16)/(3x²+48x+197) et pas ce que tu as écrit ...
On a alors : F(x)= 1/3 ln(3x² +48x+197)
I = F(2) - F(1)
I = 1/3.ln(12+96+197) - 1/3.ln(3+48+197)
I = 1/3.ln(305) - 1/3.ln(248)
Ou si on veut :
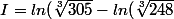)
Ou encore :
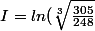)
Avec d'autres écritures possibles .

Si f(x) = (2x+16)/(3x²+48x+197) et pas ce que tu as écrit ...
On a alors : F(x)= 1/3 ln(3x² +48x+197)
I = F(2) - F(1)
I = 1/3.ln(12+96+197) - 1/3.ln(3+48+197)
I = 1/3.ln(305) - 1/3.ln(248)
Ou si on veut :
Ou encore :
Avec d'autres écritures possibles .
Re: Primitives des fonctions usuelles WIMS
merci beaucoup pour vos réponse, j'ai complètement compris grâce à vous et pour le coup j'ai eu bon, merci beaucoup !
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
