Primitive de racine carré (x+1) /

[Amcu]

Bonjour,
Rentrant en septembre En école d'ingénieur nous avions des devoirs de mathématiques pour lesquelles je n'arrive pas à trouvé la primitive de racine carré (x+1) / x
J'ai essayé de mettre la racine carré forme de puissance de 1/2 ainsi que de faire dès intégration par partie mais je tourne toujours en rond
Si vous pouviez m'aidez !?
Merci d'avance

[Razes]

Bonsoir,

Est ça ton énoncé?

[MJoe]

Bonsoir,

Est ça ton énoncé?

Bonjour,

Je suppose que :

On pose : et donc :



Remarque : il s'agit d'effectuer la décomposition d'une fraction rationnelle.





Dans le cas où le sujet indique que , on obtient :



Voici également la courbe de la fonction et de sa primitive :



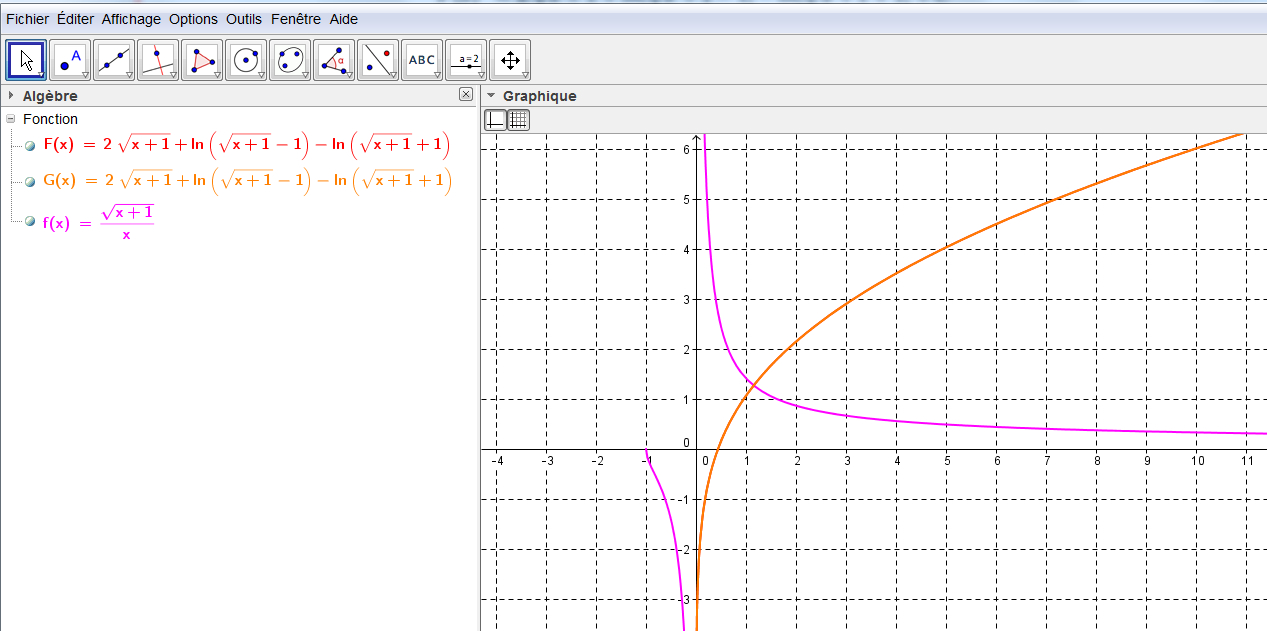
MJoe.

[Amcu]

Bonsoir,

Est ça ton énoncé?

Bonjour,

Je suppose que :

On pose : et donc :



Remarque : il s'agit d'effectuer la décomposition d'une fraction rationnelle.





Dans le cas où le sujet indique que , on obtient :



Voici également la courbe de la fonction et de sa primitive :



MJoe.

Un énorme merci c'est vrai que j'avais essayer beaucoup de chose mais Pas cette méthode qui me paraît maintenant évidente merci beaucoup d'avoir répondu aussi vite et precisement !
J'aurai une dernière petite question est ce que vous serez comment Je pourrait faire la primitive de sin(x^2+y^2) ? J'ai compris qu'il d'agissait d'une double intégration et n'ayant pas fait ça En terminale j'ai donc consultez de nombreux cours sur internet zt je pense avoir compris le principe de la double intégration mais je ne comprend pas comment je peux primitiver ceci.
J'ai tenté de décompose en sin(x^2)cos(y^2) + sin(y^2)cos(x^2) mais cela n'en mavance pas poir trouver des primitives
Ne voulant pas abuser de votre aide si Je voulez Pas répondre je comprendrai complètement
Encore un grand merci !

[zygomatique]

salut

surement faire le changement de variables :

x = r cos t
y = r sin t

et travailler sur le domaine correspondant ... faut voir ...

[MJoe]

Bonjour,

Je ne me connecte que ce soir. Aucun problème pour répondre à votre question bien sûr.

Pour votre demande d'intégrale double :

On effectue le changement de variable suivant (coordonnées polaires) :



On a un terme supplémentaire à calculer qui est le Jacobien de ce changement de variable, ce Jacobien vaut :

On peut alors écrire :





On connait une primitive de qui est

On peut donc calculer cette intégrale double.
Vous verrez également comment déterminer le domaine à partir du domaine .

Nota :
Définition du Jacobien d'un changement de variables :



Plus de détails sur les intégrales multiples et les changements de variables.

MJoe.

[Amcu]

Bonjour,

Je ne me connecte que ce soir. Aucun problème pour répondre à votre question bien sûr.

Pour votre demande d'intégrale double :

On effectue le changement de variable suivant (coordonnées polaires) :



On a un terme supplémentaire à calculer qui est le Jacobien de ce changement de variable, ce Jacobien vaut :

On peut alors écrire :





On connait une primitive de qui est

On peut donc calculer cette intégrale double.
Vous verrez également comment déterminer le domaine à partir du domaine .

Nota :
Définition du Jacobien d'un changement de variables :



Plus de détails sur les intégrales multiples et les changements de variables.

MJoe.

J'ai compris un très grand merci le domaine d'intégration était un cercle de centre 0 et de rayon racine de pie au final j'ai donc obtenue pie

[MJoe]

Bonjour,

Dans le cas où D est l'ensemble des points du cercle de centre O et de rayon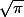 , on obtient :



On connait une primitive de qui est

On peut donc calculer cette intégrale double :









MJoe