Primitive et intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MaxBlue
- Membre Naturel
- Messages: 37
- Enregistré le: 29 Oct 2016, 01:16
-
 par MaxBlue » 07 Fév 2017, 18:55
par MaxBlue » 07 Fév 2017, 18:55
Bonjour à tous, j'ai une fonction f(x) = xe^(-x^2).
On me demande de calculer une primitive de f. Ca ne pose pas trop de problème car on applique la formule u'e^u il me semble.
Mais ensuite, la question suivante demande de calculer
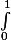
f(x) dx.
Est-ce que quelqu'un peut m'expliquer?
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 07 Fév 2017, 18:58
par lionel52 » 07 Fév 2017, 18:58
Bah c'est juste primitive en 1 - primitive en 0 !
-
MaxBlue
- Membre Naturel
- Messages: 37
- Enregistré le: 29 Oct 2016, 01:16
-
 par MaxBlue » 07 Fév 2017, 19:03
par MaxBlue » 07 Fév 2017, 19:03
Oui mais la primitive déja, comme j'ai dit "il me semble", je ne suis pas sur de ce que c'est.
On a F(x) = -2xe^(-x^2) comme primitive?
Si c'est bien ça, comment faire le calcul d'intégral? Avec une exponentielle aussi compliquée, je ne vois pas du tout comment faire en sachant que les intégrales j'ai déja du mal.

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 07 Fév 2017, 20:00
par laetidom » 07 Fév 2017, 20:00
Salut,
si

alors

et tu as

donc on devrait avoir


et lorsque tu obtiens F, pour vérifier ce résultat, tu le dérive et si tu as de nouveau f, c'est que c'est bon :
( F ) ' = f
-
MaxBlue
- Membre Naturel
- Messages: 37
- Enregistré le: 29 Oct 2016, 01:16
-
 par MaxBlue » 07 Fév 2017, 22:14
par MaxBlue » 07 Fév 2017, 22:14
Merci pour la réponse laetidom. Alors pour l'intégrale, on fait:
F(b) - F(a) = (-1/2e^-1^2) - (-1/2e^-0^2) ?
Cela donne 0.31. Est-ce que c'est bien ça?
-
Al-Kashi
- Membre Relatif
- Messages: 122
- Enregistré le: 18 Oct 2007, 00:14
-
 par Al-Kashi » 08 Fév 2017, 00:22
par Al-Kashi » 08 Fév 2017, 00:22
Salut,
Tu dois trouver

.
Si tu n'aimes pas les puissances négatives, ça donne

.
Il faut donner la valeur
exacte, sauf indication contraire de l'énoncé.
Modifié en dernier par
Al-Kashi le 08 Fév 2017, 12:52, modifié 1 fois.
-
MaxBlue
- Membre Naturel
- Messages: 37
- Enregistré le: 29 Oct 2016, 01:16
-
 par MaxBlue » 08 Fév 2017, 05:29
par MaxBlue » 08 Fév 2017, 05:29
Merci Al-Kashi, ça me parait logique et plus précis en effet.
-
Al-Kashi
- Membre Relatif
- Messages: 122
- Enregistré le: 18 Oct 2007, 00:14
-
 par Al-Kashi » 08 Fév 2017, 12:44
par Al-Kashi » 08 Fév 2017, 12:44
Je t'en prie,
Bonne journée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités