[MPSI] Polynômes de Legendre : trois questions...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
par pouik » 27 Mai 2007, 12:15
Bonjour,
Pourriez-vous m'aider à résoudre ces trois questions qui m'empèchent de poursuivre un problème. car je n'y arrive pas du tout. Merci d'avance pour votre aide.
Pout tout
,
)
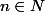
désigne le polynôme
^n)
, et
)
désigne le polynôme d'ordre
de
, i.e.
 = [(X^2-1)^n]^{(n)})
(on a dérivé
fois).
1. Soient
et
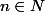
tels que
.
(a) Montrer que si
, alors
}(t)Q_n(t)dt = - \int_{-1}^{1} H_m^{(m-1)}(t)Q'_n(t)dt)
.
(b) En déduire la valeur de
Q_n(t))
(on distinguera à la fin du calcul les cas
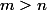
et
). Qu'en concluez-vous ?
2. Montrer qu'il existe une famille
_{n \in N})
de réels strictement positifs, que l'on explicitera, telle que
_{n \in N})
soit une base orthonormale de
.
-
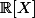
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
par pouik » 27 Mai 2007, 12:31
Oupsj'ai oublié de dire que on admet que :
 \in N^2, I_{p,q} = \int_{-1}^{1} (t-1)^p(t+1)^qdt = (-1)^p \frac{2^{p+q+1}}{(p+q+1)C_{p+q}^{p}})
Je vois bien qu'il faut s'en servir pour la première question mais je ne vois pas entièrement comment. Je vois déjà qu'on peut écrire H_n sous la forme :
 = (X-1)^n(X+1)^n)
-
SimonB
- Membre Irrationnel
- Messages: 1180
- Enregistré le: 25 Mai 2007, 21:19
-
par SimonB » 27 Mai 2007, 12:46
Pour la 1.a), une intégration par parties fonctionne bien...
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
par Edrukel » 27 Mai 2007, 14:01
salut pouik, tu ne serais pas par hasard en MPSI1 à Condorcet toi ?
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
par pouik » 27 Mai 2007, 16:37
Okay pour l'intégration par parties;
Sinon pour la 2., je trouve que :
Q_n(t)dt = -\int_{-1}^{1} Q_m^{(m-1)}Q'_n(t)dt<br />d'où : \int_{-1}^{1} Q_m(t)Q_n(t)dt = -\int_{-1}^{1} ([X^2-1]^{(m)})^{(m-1)}Q'_n(t)dt)
et donc là on trouve que :
})^{(m-1)} = (2n)!X)
d'où :
Q_n(t)dt = -\int_{-1}^{1} (2n)!X \times ([X^2-1]^{(m+1)})dt)
Est-ce correct ?
Peut-on encore simplifier plus ?
merci d'avance.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
