Polynôme de Tchebychev

[Este]

Bonjour,
En remarquant que exp(in θ)= exp(i θ)^n je dois montrer que le Polynôme de Tchebychev est égal à:
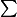
0<k<n\2 coefficients binomial(n,2k) (X^2-1)^k*X^n-2k
Ps : je n'arrive pas a utliser l’éditeur d’équation
Pouvez m'aider, je ne vois pas comment commencer

[pascal16]

Quelle définition as-tu pour le polynôme ?

[Este]

Tn(cos( θ))=cosn θ

[aviateur]

Bonjour



On développe grâçe à la formule du binôme de Newton et on simplifie.
On trouve alors que cos(nt)=P(cos(t)).

[Este]

Bonjour



On développe grâçe à la formule du binôme de Newton et on simplifie.
On trouve alors que cos(nt)=P(cos(t)).

C'est la définition que j'ai dans l’énoncé je dois montrer que c'est égale a la formule de mon premier message qui n'est pas très claire je l'accorde

[aviateur]

Non mais j'ai bien compris la question qui revient à démontrer que P(cos(t))=cos(nt) où le polynôme P est celui que tu as donné.

Il faut faire le calcul , c'est à dire développer (cos(t)+i sin(t))^n par la formule du binôme idem (cos(t)-i sin(t))^n
et simplifier.